Сумма бесконечной геометрической прогрессии равна 162, а сумма четырёх её первых членов равна 160. Найдите первый член и знаменатель прогрессии.

Ответ:

\[\left\{ \begin{matrix} \frac{b_{1}}{1 - q} = 162\ \ \ \ \ \ \ \ \ \ \\ \frac{b_{1}\left( q^{4} - 1 \right)}{q - 1} = 160 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} b_{1} = 162\ \cdot (1 - q)\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{162 \cdot (1 - q)\left( q^{4} - 1 \right)}{q - 1} = 160 \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} b_{1} = 162 \cdot (1 - q)\text{\ \ \ \ \ \ \ \ } \\ 162 \cdot \left( q^{4} - 1 \right) = - 160 \\ \end{matrix} \right.\ \]

\[q^{4} - 1 = - \frac{160}{162}\]

\[q^{4} - 1 = - \frac{80}{81}\]

\[q^{4} = \frac{1}{81}\]

\[q = \pm \frac{1}{3}.\]

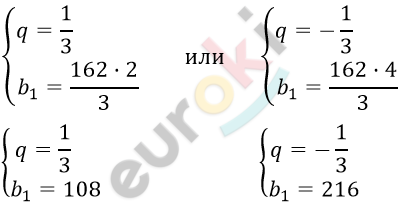
\[Ответ:q = \frac{1}{3};\]

\[b_{1} = 108\ \ или\ \ q = - \frac{1}{3};\ \ \]

\[b_{1} = 216.\]