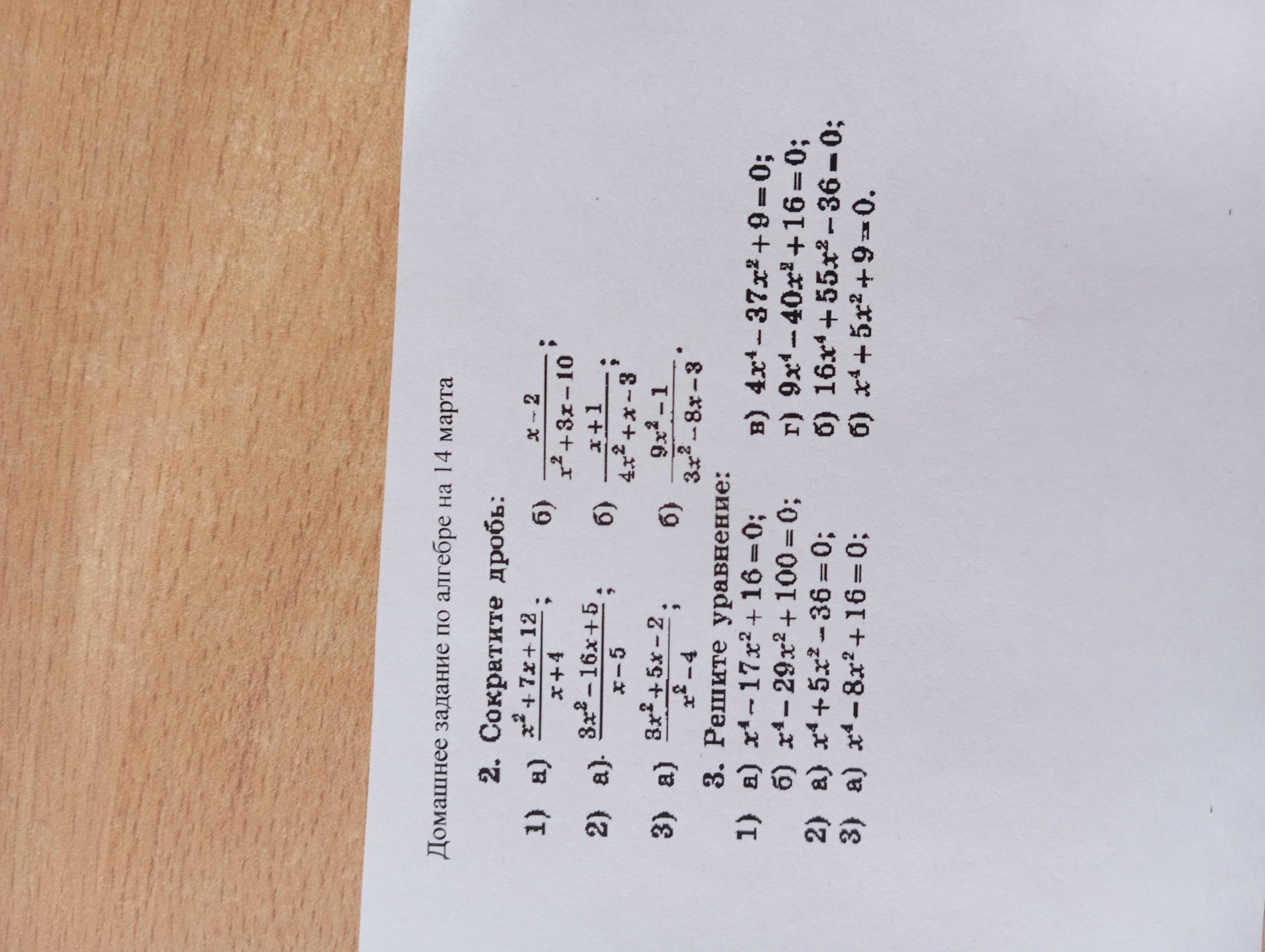
2. Сократите дробь: 1) a) $\frac{x^2 + 7x + 12}{x+4}$; б) $\frac{x-2}{x^2 + 3x - 10}$; 2) a) $\frac{3x^2 - 16x + 5}{x-5}$; б) $\frac{x+1}{4x^2 + x - 3}$; 3) a) $\frac{3x^2 + 5x - 2}{x^2 - 4}$; б) $\frac{9x^2 - 1}{3x^2 - 8x - 3}$. 3. Решите уравнение: 1) a) $x^4 - 17x^2 + 16 = 0$; в) $4x^4 - 37x^2 + 9 = 0$; 2) a) $x^4 - 29x^2 + 100 = 0$; г) $9x^4 - 40x^2 + 16 = 0$; 3) a) $x^4 + 5x^2 - 36 = 0$; б) $16x^4 + 55x^2 - 36 = 0$; 4) a) $x^4 - 8x^2 + 16 = 0$; б) $x^4 + 5x^2 + 9 = 0$.

Здравствуйте, ребята! Давайте вместе решим эти задания. **2. Сократите дробь:** 1) а) $\frac{x^2 + 7x + 12}{x+4} = \frac{(x+3)(x+4)}{x+4} = x+3$. Здесь я разложил квадратный трехчлен на множители и сократил общие множители. б) $\frac{x-2}{x^2 + 3x - 10} = \frac{x-2}{(x-2)(x+5)} = \frac{1}{x+5}$. Аналогично, разложил знаменатель на множители. 2) а) $\frac{3x^2 - 16x + 5}{x-5} = \frac{(3x-1)(x-5)}{x-5} = 3x-1$. Разложил числитель на множители. б) $\frac{x+1}{4x^2 + x - 3} = \frac{x+1}{(4x-3)(x+1)} = \frac{1}{4x-3}$. Разложил знаменатель на множители. 3) а) $\frac{3x^2 + 5x - 2}{x^2 - 4} = \frac{(3x-1)(x+2)}{(x-2)(x+2)} = \frac{3x-1}{x-2}$. Разложил числитель и знаменатель на множители. б) $\frac{9x^2 - 1}{3x^2 - 8x - 3} = \frac{(3x-1)(3x+1)}{(3x+1)(x-3)} = \frac{3x-1}{x-3}$. Разложил числитель и знаменатель на множители. **3. Решите уравнение:** 1) a) $x^4 - 17x^2 + 16 = 0$. Пусть $y = x^2$, тогда $y^2 - 17y + 16 = 0$. Решаем квадратное уравнение: $D = 17^2 - 4 \cdot 16 = 289 - 64 = 225$. $y_1 = \frac{17+15}{2} = 16$, $y_2 = \frac{17-15}{2} = 1$. Тогда $x^2 = 16$ или $x^2 = 1$. Значит, $x = \pm 4$ или $x = \pm 1$. в) $4x^4 - 37x^2 + 9 = 0$. Пусть $y = x^2$, тогда $4y^2 - 37y + 9 = 0$. $D = 37^2 - 4 \cdot 4 \cdot 9 = 1369 - 144 = 1225$. $y_1 = \frac{37 + 35}{8} = 9$, $y_2 = \frac{37 - 35}{8} = \frac{1}{4}$. Тогда $x^2 = 9$ или $x^2 = \frac{1}{4}$. Значит, $x = \pm 3$ или $x = \pm \frac{1}{2}$. 2) a) $x^4 - 29x^2 + 100 = 0$. Пусть $y = x^2$, тогда $y^2 - 29y + 100 = 0$. $D = 29^2 - 4 \cdot 100 = 841 - 400 = 441$. $y_1 = \frac{29 + 21}{2} = 25$, $y_2 = \frac{29 - 21}{2} = 4$. Тогда $x^2 = 25$ или $x^2 = 4$. Значит, $x = \pm 5$ или $x = \pm 2$. г) $9x^4 - 40x^2 + 16 = 0$. Пусть $y = x^2$, тогда $9y^2 - 40y + 16 = 0$. $D = 40^2 - 4 \cdot 9 \cdot 16 = 1600 - 576 = 1024$. $y_1 = \frac{40 + 32}{18} = 4$, $y_2 = \frac{40 - 32}{18} = \frac{4}{9}$. Тогда $x^2 = 4$ или $x^2 = \frac{4}{9}$. Значит, $x = \pm 2$ или $x = \pm \frac{2}{3}$. 3) a) $x^4 + 5x^2 - 36 = 0$. Пусть $y = x^2$, тогда $y^2 + 5y - 36 = 0$. $D = 5^2 - 4 \cdot (-36) = 25 + 144 = 169$. $y_1 = \frac{-5 + 13}{2} = 4$, $y_2 = \frac{-5 - 13}{2} = -9$. Тогда $x^2 = 4$ или $x^2 = -9$. Значит, $x = \pm 2$. б) $16x^4 + 55x^2 - 36 = 0$. Пусть $y = x^2$, тогда $16y^2 + 55y - 36 = 0$. $D = 55^2 - 4 \cdot 16 \cdot (-36) = 3025 + 2304 = 5329$. $y_1 = \frac{-55 + 73}{32} = \frac{9}{16}$, $y_2 = \frac{-55 - 73}{32} = -4$. Тогда $x^2 = \frac{9}{16}$ или $x^2 = -4$. Значит, $x = \pm \frac{3}{4}$. 4) a) $x^4 - 8x^2 + 16 = 0$. Пусть $y = x^2$, тогда $y^2 - 8y + 16 = 0$. $(y-4)^2 = 0$. $y = 4$. Тогда $x^2 = 4$. Значит, $x = \pm 2$. б) $x^4 + 5x^2 + 9 = 0$. Пусть $y = x^2$, тогда $y^2 + 5y + 9 = 0$. $D = 5^2 - 4 \cdot 9 = 25 - 36 = -11$. Так как дискриминант отрицательный, уравнение не имеет действительных решений. Надеюсь, мои объяснения вам помогли! Если у вас возникнут дополнительные вопросы, обращайтесь.