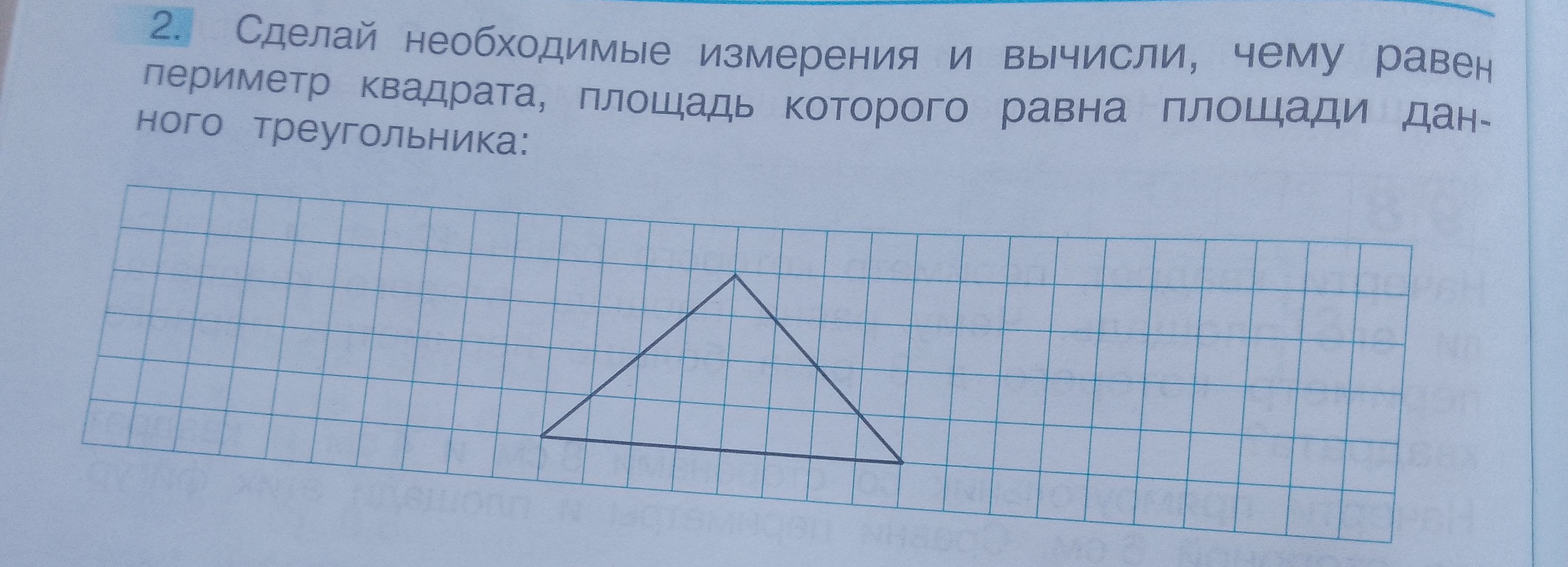
Сделай необходимые измерения и вычисли, чему равен периметр квадрата, площадь которого равна площади данного треугольника:

Давай решим эту задачу по шагам. Сначала нам нужно определить размеры треугольника на рисунке, а затем вычислить его площадь. После этого мы найдем сторону квадрата с такой же площадью и, наконец, вычислим периметр этого квадрата. 1. Измерения треугольника: По рисунку видно, что основание треугольника составляет 6 клеток, а высота – 4 клетки. Будем считать, что каждая клетка – это 1 единица измерения (например, сантиметр). - Основание (a) = 6 единиц - Высота (h) = 4 единицы 2. Вычисление площади треугольника: Площадь треугольника вычисляется по формуле: \[ S_{треугольника} = \frac{1}{2} \cdot a \cdot h \] Подставим значения: \[ S_{треугольника} = \frac{1}{2} \cdot 6 \cdot 4 = 12 \] квадратных единиц 3. Нахождение стороны квадрата: Площадь квадрата равна площади треугольника, то есть 12 квадратных единиц. Площадь квадрата вычисляется по формуле: \[ S_{квадрата} = x^2 \] Где x – сторона квадрата. Чтобы найти сторону квадрата, нужно извлечь квадратный корень из его площади: \[ x = \sqrt{S_{квадрата}} = \sqrt{12} \] \[ x = \sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3} \] единиц 4. Вычисление периметра квадрата: Периметр квадрата вычисляется по формуле: \[ P_{квадрата} = 4 \cdot x \] Подставим значение стороны квадрата: \[ P_{квадрата} = 4 \cdot 2\sqrt{3} = 8\sqrt{3} \] единиц Ответ: Периметр квадрата равен $8\sqrt{3}$ единицам. Это приблизительно равно 13.86 единицам. Развёрнутый ответ для школьника: Итак, мы начали с измерения основания и высоты треугольника. Затем вычислили площадь этого треугольника, используя формулу. После этого нашли сторону квадрата, площадь которого такая же, как у треугольника. И в конце вычислили периметр квадрата, используя найденную сторону. Важно помнить формулы площади треугольника и квадрата, а также уметь извлекать квадратный корень.