С двухметровой высоты под углом к горизонту выпущена ракета. По графику изменения высоты её полёта в зависимости от времени движения ответьте на вопросы: Какое расстояние пролетела ракета за первые 3 с полёта?

\[\ 22 + 6 = 28\ (м).\]

\[y = 5x^{2} - 8x + 3\]

\[x = - 1:\]

\[y = 5 \cdot 1 + 8 + 3 = 16.\]

\[Ответ:y = 16.\ \]

\[y = 3:\]

\[5x^{2} - 8x + 3 = 3\]

\[5x^{2} - 8x = 0\]

\[x(5x - 8) = 0\]

\[1)\ x = 0.\]

\[2)\ 5x - 8 = 0\]

\[5x = 8\]

\[x = \frac{8}{5}\]

\[x = 1,6.\]

\[Ответ:\ при\ x = 0;x = 1,6.\]

\[Нули\ функции:\]

\[5x^{2} - 8x + 3 = 0\]

\[D = 64 - 60 = 4\]

\[x_{1} = \frac{8 + 2}{10} = 1;\ \ x_{2} = \frac{8 - 2}{10} = 0,6.\]

\[Ответ:\ x_{1} = 1;x_{2} = 0,6.\]

\[\ y = x^{2} - 6x + 5\]

\[D_{1} = 9 - 5 = 4\]

\[x_{1} = 3 + 2 = 5;x_{2} = 3 - 2 = 1.\]

\[x_{0} = - \frac{b}{2a} = \frac{6}{2} = 3;\]

\[y_{0} = 9 - 18 + 5 = - 4.\]

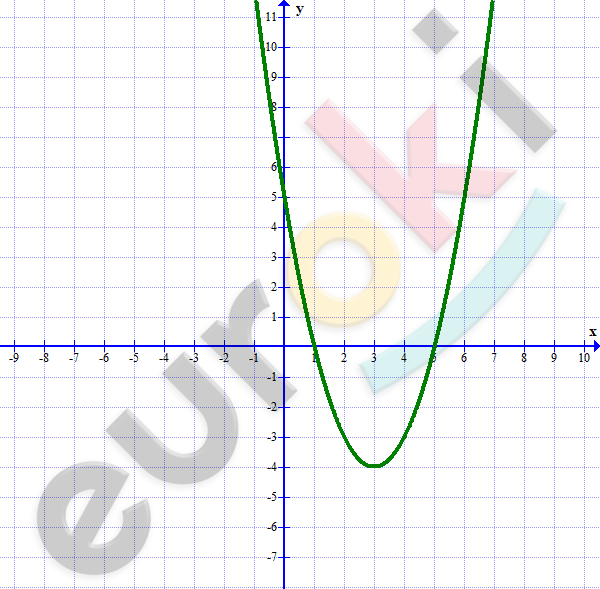
\[x \in ( - \infty;1) \cup (5;\ + \infty).\]

\[Функция\ возрастает\ на\ промежутке\]

\[\lbrack 3; + \infty).\]

\[x^{2} - 4x - 5 < 0\]

\[D_{1} = 4 + 5 = 9\]

\[x_{1} = 2 + 3 = 5;x_{2} = 2 - 3 = - 1.\]

\[(x + 1)(x - 3) < 0\]

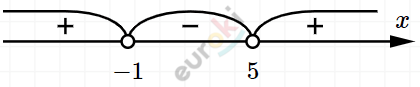
\[x \in ( - 1;5).\]

\[Ответ:\ x \in ( - 1;5).\]

\[y = \sqrt{25 - x^{2}}\]

\[ООФ:\]

\[25 - x^{2} \geq 0\]

\[x^{2} - 25 \leq 0\]

\[(x + 5)(x - 5) \leq 0\]

\[x \in \lbrack - 5;5\rbrack.\]

\[Ответ:\ x \in \lbrack - 5;5\rbrack.\]

\[y = 2x^{2}\]

\[y = 2 \cdot (x + 3)^{2} - 1 =\]

\[= 2 \cdot \left( x^{2} + 6x + 9 \right) - 1 =\]

\[= 2x^{2} + 12x + 18 - 1 =\]

\[= 2x^{2} + 12x + 17.\]

\[Уравнение\ параболы:\]

\[y = 2x^{2} + 12x + 17.\]

\[y = 3x^{2} + bx + c;вершина\ (1; - 2):\]

\[x_{0} = - \frac{b}{2a}\]

\[1 = - \frac{b}{6}\]

\[b = - 6.\]

\[y_{0} = 3x^{2} + bx + c\]

\[- 2 = 3 \cdot 1^{2} + ( - 6) \cdot 1 + c\]

\[c = - 2 - 3 + 6\]

\[c = 1.\]

\[Ответ:b = - 6;\ \ c = 1.\]