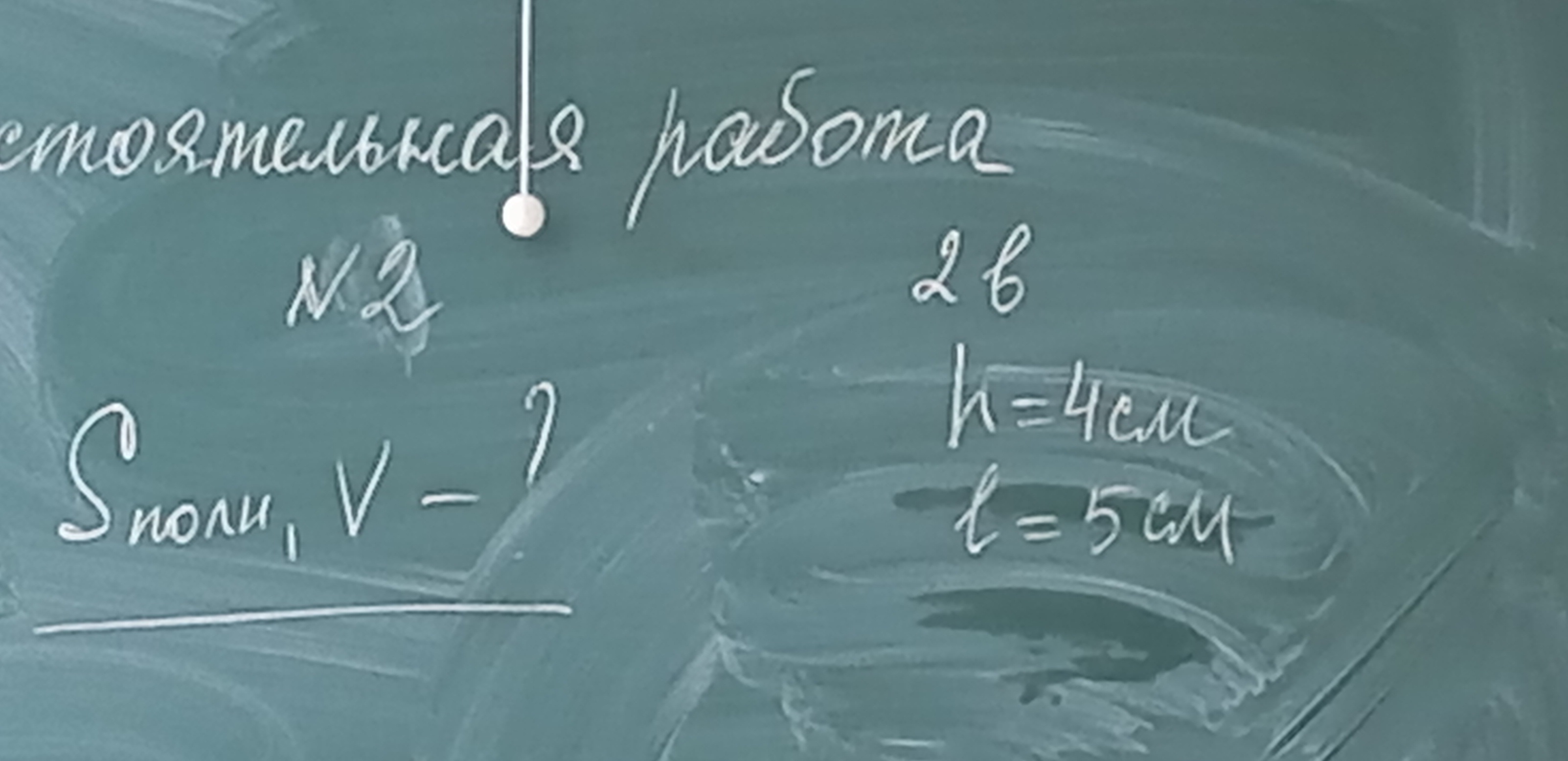
Вопрос:
Решите задачу, представленную на доске. Найдите площадь полной поверхности и объем прямоугольного параллелепипеда, если его высота h = 4 см, а длина l = 5 см.
Ответ:
Здравствуйте, ребята! Давайте решим эту задачу вместе.
**Задача:** Найти площадь полной поверхности ($S_{полн}$) и объем ($V$) прямоугольного параллелепипеда, если его высота $h = 4$ см и длина $l = 5$ см.
Но для начала нам нужно понять, что такое прямоугольный параллелепипед и какие формулы нам понадобятся.
Прямоугольный параллелепипед – это объемная фигура, у которой шесть граней, и каждая грань – прямоугольник.
Для решения задачи нам потребуются следующие формулы:
1. Площадь полной поверхности прямоугольного параллелепипеда:
$S_{полн} = 2(ab + bc + ac)$, где a, b, c - длины сторон параллелепипеда.
2. Объем прямоугольного параллелепипеда:
$V = abc$, где a, b, c - длины сторон параллелепипеда.
**Решение:**
К сожалению, у нас недостаточно данных для решения задачи. У нас есть только высота (h = 4 см) и длина (l = 5 см), но нет ширины. Обозначим ширину как "w".
Предположим, что ширина (w) нам известна и равна, к примеру, 3 см. Тогда можем решить задачу.
1. **Находим площадь полной поверхности:**
$S_{полн} = 2(lw + wh + lh) = 2(5 \cdot 3 + 3 \cdot 4 + 5 \cdot 4) = 2(15 + 12 + 20) = 2(47) = 94$ см$^2$
Таким образом, площадь полной поверхности равна 94 см$^2$.
2. **Находим объем:**
$V = lwh = 5 \cdot 3 \cdot 4 = 60$ см$^3$
Следовательно, объем равен 60 см$^3$.
**Ответ:**
Если ширина равна 3 см, то:
* Площадь полной поверхности: **94 см$^2$**
* Объем: **60 см$^3$**
**Важно:** Для решения задачи необходимо знать все три измерения прямоугольного параллелепипеда (длину, ширину и высоту). Если в условии задачи не хватает данных, нужно запросить их или сделать предположение, как это сделали мы, указав, что ширина равна 3 см.