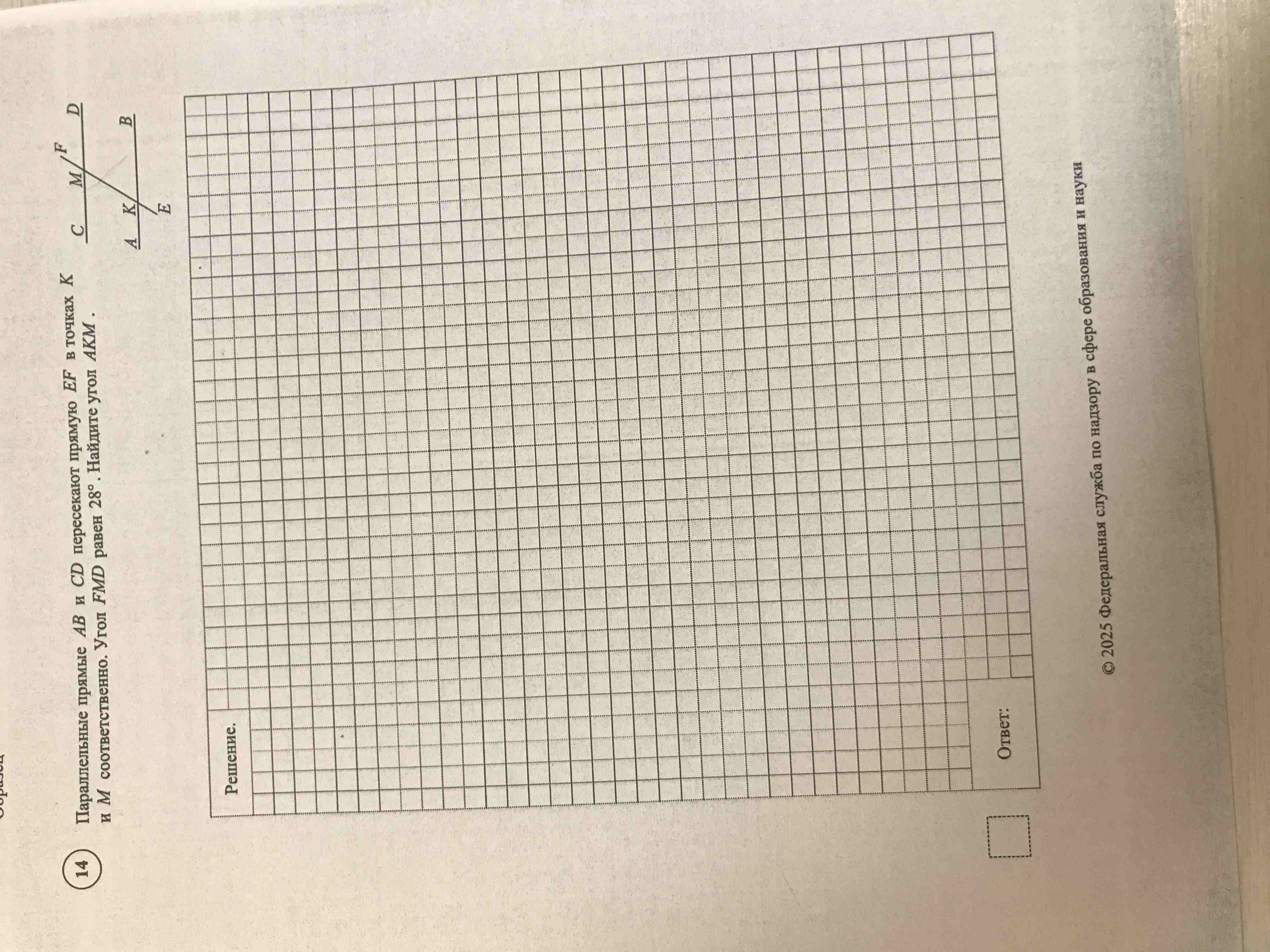
Вопрос:
Решите задачу: Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28°. Найдите угол AKM.
Ответ:
Здравствуйте, ребята! Давайте решим эту задачу вместе.
**Дано:**
* AB || CD (AB параллельна CD)
* EF пересекает AB в точке K
* EF пересекает CD в точке M
* ∠FMD = 28°
**Найти:** ∠AKM
**Решение:**
1. **Определение углов:**
* ∠FMD и ∠CME – смежные углы. Сумма смежных углов равна 180°.
* ∠AKM и ∠BKM – смежные углы. Сумма смежных углов равна 180°.
2. **Находим ∠CME:**
Так как ∠FMD и ∠CME смежные, то:
∠CME = 180° - ∠FMD = 180° - 28° = 152°
3. **Применяем свойство параллельных прямых:**
Так как AB || CD и EF – секущая, то ∠AKM и ∠CME – соответственные углы. Соответственные углы при параллельных прямых равны.
Следовательно, ∠AKM = ∠CME
4. **Вывод:**
∠AKM = 152°
**Ответ:** ∠AKM = 152°
Теперь давайте запишем это в более формальном виде с использованием MathJax:
1. \( \angle CME = 180^\circ - \angle FMD \)
2. \( \angle CME = 180^\circ - 28^\circ = 152^\circ \)
3. Так как AB || CD, то \( \angle AKM = \angle CME = 152^\circ \)
**Ответ:** \( \angle AKM = 152^\circ \)
Надеюсь, теперь вам понятно, как решать такие задачи! Если у вас возникнут вопросы, не стесняйтесь спрашивать.
**Развернутый ответ для школьника:**
Представьте, что у вас есть две параллельные дороги (AB и CD). Эти дороги пересекает одна прямая улица (EF). Точки пересечения - это места, где улицы встречаются. Нам известно, что один из углов, образованных пересечением (∠FMD), равен 28 градусам. Нужно найти другой угол (∠AKM).
Сначала мы находим угол, который находится рядом с известным углом (∠CME). Так как они вместе образуют прямую линию, их сумма равна 180 градусам. Зная это, мы вычитаем известный угол из 180, чтобы найти ∠CME.
Затем, мы используем важное правило: когда параллельные прямые пересекаются прямой линией, углы в одинаковых позициях (соответственные углы) равны. Значит, угол, который мы ищем (∠AKM), равен углу, который мы нашли (∠CME).
Таким образом, мы нашли, что ∠AKM равен 152 градусам. Это как найти одинаковые кусочки пазла в разных местах рисунка!