Решите уравнение: (x-2)(x-1)(x+5)(x+6)=120.

\[(x - 2)(x - 1)(x + 5)(x + 6) =\]

\[= 120\]

\[(x - 2)(x + 6)(x - 1)(x + 5) =\]

\[= 120\]

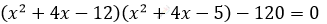
\[t = x^{2} + 4x - 5\]

\[(t - 7)t - 120 = 0\]

\[t^{2} - 7t - 120 = 0\]

\[D = ( - 7)^{2} - 4 \cdot 1 \bullet ( - 120) =\]

\[= 49 + 480 = 529\]

\[t_{1} = \frac{7 + \sqrt{529}}{2} = \frac{7 + 23}{2} = \frac{30}{2} =\]

\[= 15\]

\[t_{2} = \frac{7 - \sqrt{529}}{2} = \frac{7 - 23}{2} =\]

\[= \frac{- 16}{2} = - 8\]

\[1)\ x^{2} + 4x - 5 = 15\]

\[x^{2} + 4x - 20 = 0\]

\[D = 4^{2} - 4 \cdot 1 \cdot ( - 20) =\]

\[= 16 + 80 = 96\]

\[x_{1} = \frac{- 4 + \sqrt{96}}{2} = \frac{- 4 + 4\sqrt{6}}{2} =\]

\[= - 2 + 2\sqrt{6}\]

\[x_{2} = \frac{- 4 - \sqrt{96}}{2} = \frac{- 4 - 4\sqrt{6}}{2} =\]

\[= - 2 - 2\sqrt{6}\]

\[2)\ x^{2} + 4x - 5 = - 8\]

\[x^{2} + 4x + 3 = 0\]

\[D = 4^{2} - 4 \cdot 1 \cdot 3 = 16 - 12 = 4\]

\[x_{1} = \frac{- 4 + \sqrt{4}}{2} = \frac{- 4 + 2}{2} = \frac{- 2}{2} =\]

\[= - 1\]

\[x_{2} = \frac{- 4 - \sqrt{4}}{2} = \frac{- 4 - 2}{2} = \frac{- 6}{2} =\]

\[= - 3\]

\[Ответ:\ - 2 + 2\sqrt{6};\ \ - 2 - 2\sqrt{6};\ \]

\[\ - 1;\ - 3.\]