Решите уравнение: x^3-2x^2-8x+16=0.

\[x^{3} - 2x^{2} - 8x + 16 = 0\]

\[x\left( x^{2} - 8 \right) - 2 \cdot \left( x^{2} - 8 \right) = 0\]

\[\left( x^{2} - 8 \right)(x - 2) = 0\]

\[\left( x - \sqrt{8} \right)\left( x + \sqrt{8} \right)(x - 2) = 0\]

\[\left( x - 2\sqrt{2} \right)\left( x + 2\sqrt{2} \right)(x - 2) = 0\]

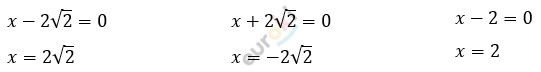
\[Ответ:2\sqrt{2};\ - 2\sqrt{2};2.\]