Решите уравнение: 3x/(x^2+2x+1)-3/(x^3+2x^2+x)=5/(2x^2+2x).

\[\frac{3x}{x^{2} + 2x + 1} - \frac{3}{x^{3} + 2x^{2} + x} =\]

\[= \frac{5}{2x^{2} + 2x}\]

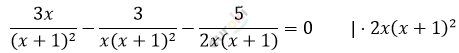
\[x \neq 0;\ \ \ \ \ \ \ \ \ \ \ x \neq - 1\]

\[3x \cdot 2x - 3 \cdot 2 - 5 \cdot (x + 1) = 0\]

\[6x^{2} - 6 - 5x - 5 = 0\]

\[6x^{2} - 5x - 11 = 0\]

\[D = ( - 5)^{2} - 4 \cdot 6 \cdot ( - 11) =\]

\[= 25 + 264 = 289;\ \ \ \ \ \sqrt{D} = 17.\]

\[x_{1} = \frac{5 + 17}{2 \cdot 6} = \frac{22}{12} = \frac{11}{6} = 1\frac{5}{6}\]

\[x_{2} = \frac{5 - 17}{2 \cdot 6} = \frac{- 12}{12} =\]

\[= - 1\ \ (не\ подходит).\]

\[Ответ:1\frac{5}{6}.\]