Решите уравнение методом замены переменной: (x-3)/(x+2)+(x+2)/(x-3)=41/4.

Ответ:

\[\frac{x - 3}{x + 2} + \frac{x + 2}{x - 3} = 4\frac{1}{4}\]

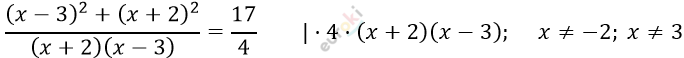
\[4 \cdot (x - 3)^{2} + 4 \cdot (x + 2)^{2} =\]

\[= 17 \cdot (x + 2)(x - 3)\]

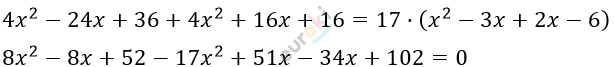
\[- 9x^{2} + 9x + 154 = 0\]

\[9x^{2} - 9x - 154 = 0\]

\[D = 81 + 5544 = 5625 = 75^{2}\]

\[x_{1} = \frac{9 + 75}{18} = \frac{84}{18} = 4\frac{2}{3};\ \ \ \ \ \ \]

\[x_{2} = \frac{9 - 75}{18} = - \frac{66}{18} = - 3\frac{2}{3}.\]

\[Ответ:x = 4\frac{2}{3};\ x = - 3\frac{2}{3}\text{.\ }\]