Решите уравнение методом замены переменной: 8/(x^2-6x+12)-x^2+6x=10.

Ответ:

\[\frac{8}{x^{2} - 6x + 12} - x^{2} + 6x = 10\]

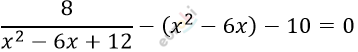
\[Пусть\ x^{2} - 6x + 12 = t:\]

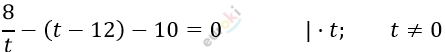
\[8 - t \cdot (t - 12) - 10t = 0\]

\[8 - t^{2} + 12t - 10t = 0\]

\[8 - t^{2} + 2t = 0\]

\[t^{2} - 2t - 8 = 0\]

\[t_{1} + t_{2} = 2\]

\[t_{1} \cdot t_{2} = - 8\]

\[\Longrightarrow t_{1} = 4,\ \ t_{2} = - 2.\]

\[Ответ:x = 4;x = 2.\]