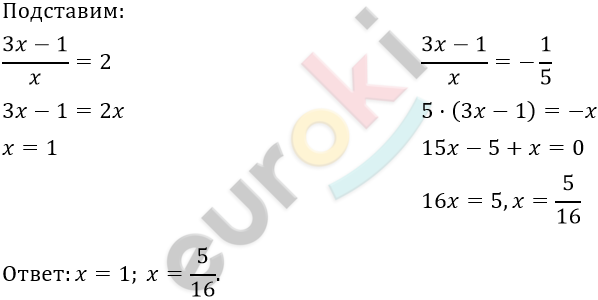Решите уравнение методом замены переменной: (3x-1)/x-2x/5(3x-1)=9/5.

Ответ:

\[\frac{3x - 1}{x} - \frac{2x}{5 \cdot (3x - 1)} = \frac{9}{5}\]

\[Пусть\ \ t = \frac{3x - 1}{x};\ \ x \neq 0;\ \ \]

\[x \neq \frac{1}{3}:\]

\[t - \frac{2}{5} \cdot \frac{1}{t} - \frac{9}{5} = 0\ \ \ \ \ \ \ \ \ \ | \cdot 5t\]

\[5t^{2} - 9t - 2 = 0\]

\[D = 81 + 40 = 121\]

\[t_{1} = \frac{9 + 11}{10} = 2;\ \ \ \ \]

\[t_{2} = \frac{9 - 11}{10} = - \frac{2}{10} = - \frac{1}{5}.\]