Решите уравнение: корень из (4x-3)-корень из (2x-2)=1.
Ответ:
\[\sqrt{4x - 3} - \sqrt{2x - 2} = 1\]
\[u = \sqrt{4x - 3};\ \ \ v = \sqrt{2x - 2}\]
\[u - v = 1\]
\[{2u}^{2} - 4v^{2} =\]
\[= 2 \cdot (4x - 3) - 4 \cdot (2x - 2) =\]
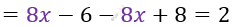
\[\left\{ \begin{matrix} u - v = 1\ \ \ \ \ \ \ \ \ \\ 2u^{2} - 4v^{2} = 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} u = v + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 2 \cdot (v + 1)^{2} - 4v^{2} = 2 \\ \end{matrix} \right.\ \]
\[2v^{2} + 4v + 2 - 4v^{2} - 2 = 0\]
\[- 2v^{2} + 4v = 0\]
\[- 2v(v - 2) = 0\]
\[\left\{ \begin{matrix} v_{1} = 0 \\ u_{1} = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} v_{2} = 2 \\ u_{2} = 3 \\ \end{matrix} \right.\ \]
\[1)\ \left\{ \begin{matrix} \sqrt{2x - 2} = 0 \\ \sqrt{4x - 3} = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 2x - 2 = 0 \\ 4x - 3 = 1 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 2x = 2 \\ 4x = 4 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} x = 1 \\ x = 1 \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} \sqrt{2x - 2} = 2 \\ \sqrt{4x - 3} = 3 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 2x - 2 = 4 \\ 4x - 3 = 9 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 2x = 6\ \ \\ 4x = 12 \\ \end{matrix} \right.\ \text{\ \ \ \ }\]
\[\left\{ \begin{matrix} x = 3 \\ x = 3 \\ \end{matrix} \right.\ \]
\[Ответ:\ \ 1;3.\]