Решите уравнение: (4x+1)/(x-3)=(3x-8)/(x+1).

Ответ:

\[\frac{4x + 1}{x - 3} = \frac{3x - 8}{x + 1}\]

\[ОДЗ:\ \ x \neq 3\]

\[\ \ \ \ \ \ \ \ \ \ \ \ x \neq - 1\]

\[\frac{4x + 1}{x - 3} - \frac{3x - 8}{x + 1} = 0\]

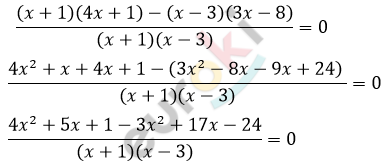
\[\frac{x^{2} + 22x - 23}{(x + 1)(x - 3)} = 0\]

\[x_{1} + x_{2} = - 22\]

\[x_{1} \cdot x_{2} = - 23 \Longrightarrow x_{1} = - 23;\ \ \ \]

\[x_{2} = 1\]

\[Ответ:\ \ x = - 23\ \ \ \ и\ \ \ x = 1.\]