На двух станках отштамповали 1300 деталей за 13 ч. Известно, что 120 деталей на первом станке штампуют на 1 ч быстрее, чем на втором. Сколько деталей в час штампуют на первом станке?

\[Пусть\ x\ деталей\ в\ час -\]

\[производительность\ первого\ \]

\[станка;\]

\[1300\ :13 =\]

\[= 100\ (\frac{дет}{ч) - вместе.}\]

\[(100 - x)деталей\ в\ час -\]

\[производительность\ второго\ \]

\[станка.\]

\[Известно,\ что\ на\ каждом\ \]

\[станке\ было\ сделано\ по\ \]

\[120\ деталей.\]

\[Составим\ уравнение:\]

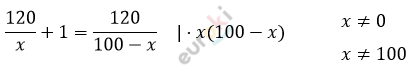
\[120 \cdot (100 - x) + x(100 - x) =\]

\[= 120x\]

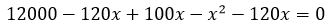
\[- x^{2} - 140x + 12000 = 0\]

\[x^{2} + 140x - 12000 = 0\]

\[D = 140^{2} - 4 \cdot 1 \cdot ( - 12000) =\]

\[= 19600 + 48000 = 67600;\ \ \]

\[\sqrt{D} = 260\]

\[x_{1} = \frac{- 140 + 260}{2} = \frac{120}{2} =\]

\[= 60\ (деталей\ в\ час) -\]

\[производительность\ первого\ \]

\[станка.\]

\[x_{2} = \frac{- 140 - 260}{2} = \frac{- 400}{2} =\]

\[= - 200\ (не\ подходит).\]

\[Ответ:60\ деталей\ в\ час.\]