Решите уравнение (20y)/(36y^2-4)-(2y-3)/(2-6y)=(5-2y)/(6y+2).

\[а)\ \frac{20y}{36y^{2} - 4} - \frac{2y - 3^{\backslash 6y + 2}}{2 - 6y} = \frac{5 - 2y^{\backslash 6y - 2}}{6y + 2}\]

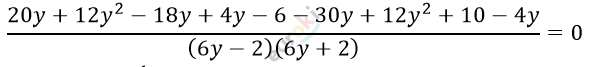
\[ОДЗ:\ \ \ y \neq \pm \frac{1}{3}.\]

\[24y^{2} - 28y + 4 = 0\ \ \ \ \ \ \ |\ :4\]

\[6y^{2} - 7y + 1 = 0\]

\[D = 49 - 24 = 25\]

\[y_{1} = \frac{7 + 5}{12} = 1;\ \ \ \ \ \]

\[y_{2} = \frac{7 - 5}{12} = \frac{2}{12} = \frac{1}{6}.\]

\[Ответ:y = \frac{1}{6};\ \ y = 1.\]