Решите уравнение: |x-3|(x^2+4x-1)=4*(x-3).

\[|x - 3|\left( x^{2} + 4x - 1 \right) =\]

\[= 4 \bullet (x - 3)\]

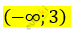
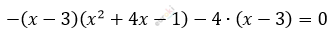
\[(x - 3)\left( - x^{2} - 4x + 1 - 4 \right) = 0\]

\[(x - 3)\left( - x^{2} - 4x - 3 \right) = 0\]

\[(x - 3)\left( x^{2} + 4x + 3 \right) = 0\]

\[x = 3 \Longrightarrow \ \ не\ подходит.\]

\[x^{2} + 4x + 3 = 0\]

\[D = 4^{2} - 4 \cdot 1 \cdot 3 = 16 - 12 = 4\]

\[x_{1} = \frac{- 4 + \sqrt{4}}{2} = \frac{- 4 + 2}{2} = \frac{- 2}{2} =\]

\[= - 1\]

\[x_{2} = \frac{- 4 - \sqrt{4}}{2} = \frac{- 4 - 2}{2} = \frac{- 6}{2} =\]

\[= - 3.\]

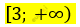
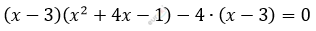
\[(x - 3)\left( x^{2} + 4x - 1 - 4 \right) = 0\]

\[(x - 3)\left( x^{2} + 4x - 5 \right) = 0\]

\[x = 3.\]

\[x^{2} + 4x - 5 = 0\]

\[D = 4^{2} - 4 \cdot 1 \cdot ( - 5) =\]

\[= 15 + 20 = 36\]

\[x_{1} = \frac{- 4 + \sqrt{36}}{2} = \frac{- 4 + 6}{2} = \frac{2}{2} =\]

\[= 1 \Longrightarrow \ \ не\ подходит.\]

\[x_{2} = \frac{- 4 - \sqrt{36}}{2} = \frac{- 4 - 6}{2} =\]

\[= \frac{- 10}{2} = - 5 \Longrightarrow \ \ не\ подходит.\]

\[Ответ:\ - 1;\ - 3;\ 3.\]