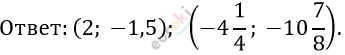Решите систему уравнений: 3x-2y=9; 4x^2+6y=7.

Ответ:

\[\left\{ \begin{matrix} 3x - 2y = 9\ \ | \cdot 3 \\ 4x^{2} + 6y = 7\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 9x - 6y = 27 \\ 4x^{2} + 6y = 7\ \\ \end{matrix} \right.\ ( + )\text{\ \ }\]

\[\left\{ \begin{matrix} 4x² + 9x - 34 = 0 \\ y = \frac{3x - 9}{2}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

\[4x^{2} + 9x - 34 = 0\]

\[D = 81 + 544 = 625\]

\[x_{1} = \frac{- 9 + 25}{8} = 1,\ \ \]

\[x_{2} = \frac{- 9 - 25}{8} = - 4\frac{1}{4}\]

\[\left\{ \begin{matrix} x = 2\ \ \ \ \ \ \\ y = - 1,5 \\ \end{matrix} \right.\ \ \ \ \ \ или\ \ \ \ \]

\[\left\{ \begin{matrix} x = - 4\frac{1}{4}\text{\ \ \ \ \ \ \ \ \ } \\ y = \frac{- \frac{51}{4} - \frac{36}{4}}{2} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = - 4\frac{1}{4} \\ y = - \frac{87}{8} \\ \end{matrix} \right.\ \text{\ \ \ \ \ }\]

\[\left\{ \begin{matrix} x = - 4\frac{1}{4\ }\ \\ y = - 10\frac{7}{8} \\ \end{matrix} \right.\ \]