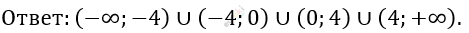Решите неравенство: ((x-3)/(x+4))^2+((x+3)/(x-4))^2>(2x^2-18)/(x^2-16).

\[\left( \frac{x - 3}{x + 4} \right)^{2} + \left( \frac{x + 3}{x - 4} \right)^{2} > \frac{2x^{2} - 18}{x^{2} - 16\ }\]

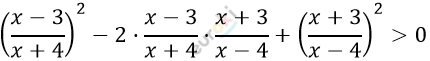
\[\left( \frac{x - 3^{\backslash x - 4}}{x + 4} - \frac{x + 3^{\backslash x + 4}}{x - 4} \right)^{2} > 0\]

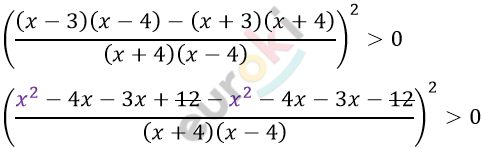
\[\left( \frac{- 14x}{(x + 4)(x - 4)} \right)^{2} > 0\]

\[\frac{196x^{2}}{(x + 4)^{2}(x - 4)^{2}} > 0\]