Решите неравенство: (11-2корень из 24)x>корень из 8-корень из 3.

\[\left( 11 - 2\sqrt{24} \right)x > \sqrt{8} - \sqrt{3}\]

\[\left( \sqrt{8} - \sqrt{3} \right)^{2}x > \sqrt{8} - \sqrt{3}\]

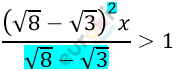
\[\left( \sqrt{8} - \sqrt{3} \right)x > 1\]

\[x > \frac{1}{\sqrt{8} - \sqrt{3}}\]

\[\frac{1}{\sqrt{8} - \sqrt{3}} =\]

\[= \frac{\sqrt{8} + \sqrt{3}}{\left( \sqrt{8} - \sqrt{3} \right)\left( \sqrt{8} + \sqrt{3} \right)} =\]

\[= \frac{\sqrt{8} + \sqrt{3}}{8 - 3} = \frac{\sqrt{8} + \sqrt{3}}{5}\]

\[x > \frac{\sqrt{8} + \sqrt{3}}{5}\]

\[Ответ:\ \ \left( \frac{\sqrt{8} + \sqrt{3}}{5}; + \infty \right).\]