Решите неравенство (-корень из x-x)(x-6корень из x+8)>=0.

\[\left( - \sqrt{x} - x \right)\left( x - 6\sqrt{x} + 8 \right) \geq 0\ \ \ \ \ \ \ \ \ \]

\[Пусть\ \ t = \sqrt{x};\ \ t \geq 0:\]

\[\left( - t - t^{2} \right)\left( t^{2} - 6t + 8 \right) \geq 0\]

\[t^{2} - 6t + 8 = 0\]

\[t_{1} = 4;\ \ \ t_{2} = 2\]

\[- t(t + 1)(t - 4)(t - 2) \geq 0\]

\[t(t + 1)(t - 4)(t - 2) \leq 0\]

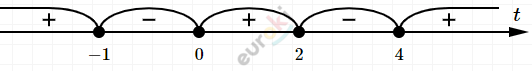
\[- 1 \leq t \leq 0 \Longrightarrow t = 0\]

\[2 \leq t \leq 4\]

\[\sqrt{x} = 0 \Longrightarrow x = 0\]

\[2 \leq \sqrt{x} \leq 4 \Longrightarrow 4 \leq x \leq 16.\]

\[Ответ:\left\{ 0 \right\} \cup \lbrack 4;16\rbrack.\]