Разность пятого и третьего членов геометрической прогрессии равна 1200, а разность пятого и четвёртого членов равна 1000. Найдите сумму пяти первых членов прогрессии.

Ответ:

\[\left\{ \begin{matrix} b_{5} - b_{3} = 1200 \\ b_{5} - b_{4} = 1000 \\ \end{matrix}\text{\ \ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} b_{1}q^{4} - b_{1}q^{2} = 1200 \\ b_{1}q^{4} - b_{1}q^{3} = 1000 \\ \end{matrix}\text{\ \ \ \ \ \ \ } \right.\ \]

\[\left\{ \begin{matrix} b_{1}q^{2}\left( q^{2} - 1 \right) = 1200 \\ b_{1}q^{3}(q - 1) = 1000 \\ \end{matrix} \right.\ \]

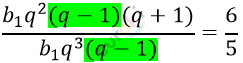
\[\frac{q + 1}{q} = \frac{6}{5}\]

\[5q + 5 - 6q = 0\]

\[q = 5.\]

\[b_{1} = \frac{1200}{24 \cdot 25} = 2.\]

\[S_{5} = \frac{2 \cdot \left( 5^{5} - 1 \right)}{5 - 1} =\]

\[= \frac{2 \cdot 3124}{4} = 1562.\]

\[Ответ:1562.\ \ \]