При каком положительном значении параметра p один из корней квадратного уравнения x^2-px+48=0 в 3 раза больше другого?

\[x^{2} - px + 48 = 0\]

\[D = p^{2} - 4 \cdot 48 = p^{2} - 192\]

\[Так\ как\ уравнение\ имеет\ \]

\[2\ корня,\ то\ D > 0.\]

\[x_{1,2} = \frac{p \pm \sqrt{p² - 192}}{2}\]

\[По\ условию\ \ \ x_{1} = 3x_{2}:\]

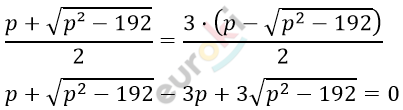
\[2p - 4\sqrt{p^{2} - 192} = 0\]

\[(p)^{2} = \left( 2\sqrt{p^{2} - 192} \right)^{2}\]

\[p^{2} = 4p^{2} - 768\]

\[3p^{2} = 768\]

\[p^{2} = 256\]

\[p = \pm 16\]

\[Так\ как\ p > 0,\ \ \ то\ \ p = 16.\]

\[Ответ:p = 16.\]