При каких значениях параметра p неравенство: px^2+(2p-3)x+(p+3)>0 верно при всех значениях x?

\[px^{2} + (2p - 3)x + (p + 3) > 0\]

\[Верно\ при\ всех\ x,\ если:\]

\[\left\{ \begin{matrix} p > 0 \\ D < 0 \\ \end{matrix} \right.\ \]

\[D = (2p - 3)^{2} - 4p(p + 3) < 0\]

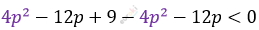
\[- 24p + 9 < 0\]

\[- 24p < - 9\]

\[p > \frac{9}{24}\]

\[p > \frac{3}{8}\]

\[\left\{ \begin{matrix} p > 0 \\ p > \frac{3}{8} \\ \end{matrix} \right.\ \]

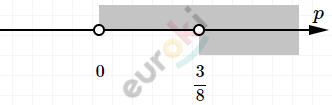
\[Ответ:при\ p \in \left( \frac{3}{8};\ + \infty \right).\]