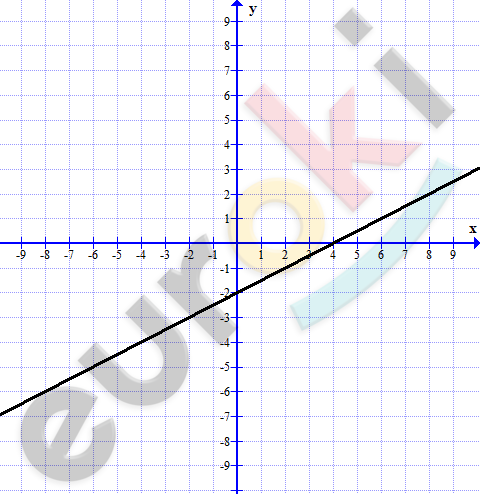
Постройте график функции: y=1/2 x-2. С помощью определения докажите, что функция y=1/2 x-2 является возрастающей на множестве R.

\[y = \frac{1}{2}x - 2\]

\[x_{1} < x_{2} \Longrightarrow y_{1} - y_{2} =\]

\[= \frac{1}{2}x_{1} - 2 - \left( \frac{1}{2}x_{2} - 2 \right) =\]

\[= \frac{1}{2}x_{1} - 2 - \frac{1}{2}x_{2} + 2 =\]

\[= \frac{1}{2}x_{1} - \frac{1}{2}x_{2} = \frac{1}{2} \cdot \left( x_{1} - x_{2} \right) < 0;\]

\[y_{1} - y_{2} < 0 \Longrightarrow y_{1} < y_{2} \Longrightarrow y =\]

\[= \frac{1}{2}x - 2\ возрастает\ на\ R.\]