Поезд был задержан на станции на 12 мин. Чтобы пройти участок пути в 60 км без опоздания, машинист увеличил скорость поезда на 10 км/ч. С какой скоростью шел поезд?

\[\text{x\ }\frac{км}{ч} - скорость\ до\ станции;\]

\[(x + 10)\ \frac{км}{ч} - скорость\ \]

\[после\ станции.\]

\[12\ мин = \frac{1}{5}\ ч.\]

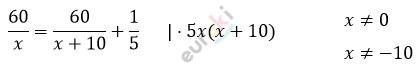
\[60 \cdot 5 \cdot (x + 10) =\]

\[= 60 \cdot 5x + x(x + 10)\]

\[300 \cdot (x + 10) =\]

\[= 300x + x^{2} + 10x\]

\[300x + 3000 - 300x = x^{2} + 10x\]

\[x^{2} + 10x - 3000 = 0\]

\[D = 10^{2} - 4 \cdot 1 \cdot ( - 3000) =\]

\[= 100 + 12\ 000 = 12\ 100;\ \ \]

\[\sqrt{D} = 110.\]

\[x_{1} = \frac{- 10 + 110}{2} = \frac{100}{2} = 50;\ \ \ \]

\[x_{2} = \frac{- 10 - 110}{2} = - \frac{120}{2} =\]

\[= - 60\ (не\ подходит)\ \]

\[x + 10 = 50 + 10 =\]

\[= 60\ \left( \frac{км}{ч} \right) - скорость\ после\]

\[\ станции.\]

\[Ответ:60\frac{км}{ч}.\]