Постройте график функции у = x2: Докажите, что эта функция является убывающей на промежутке (–∞; 0].

\[y = x^{2}.\]

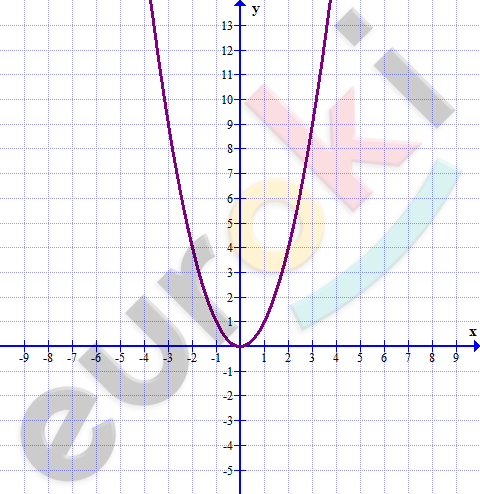
\[( - \infty;0\rbrack:\]

\[x_{1} < x_{2} \leq 0 \Longrightarrow y_{1} - y_{2} =\]

\[= x_{1}^{2} - x_{2}^{2} =\]

\[= \left( x_{1} - x_{2} \right)\left( x_{1} + x_{2} \right) > 0;\]

\[y_{1} - y_{2} > 0 \Longrightarrow y_{1} > y_{2} \Longrightarrow\]

\[\Longrightarrow y = x^{2} - убывает\ на\]

\[\ ( - \infty;0\rbrack. \]

\[y = x^{2}.\]

\[x \in \lbrack - 5;7\rbrack:\]

\[x = - 5 \Longrightarrow y = ( - 5)^{2} = 25.\]

\[x = 0 \Longrightarrow y = 0.\]

\[x = 7 \Longrightarrow y = 7^{2} = 49.\]

\[y \in \lbrack 0;49\rbrack.\]