Первая, вторая и третья бригады, работая отдельно, выполнят задание за а, b и с дней соответственно, а при совместной работе они выполнят то же задание за t дней. Какому числовому промежутку наименьшей длины принадлежат значения t, если 3 ≤ а ≤ 5, 8 ≤ b ≤ 10 и 24 ≤ с ≤ 30?

\[Пусть\ 1 - все\ задание.\]

\[\frac{1}{a} - первая\ за\ 1\ день;\]

\[\frac{1}{b} - вторая\ за\ 1\ день;\]

\[\frac{1}{c} - третья\ за\ 1\ день.\]

\[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{t} - совместная\ \]

\[производительность.\]

\[3 \leq a \leq 5\]

\[\frac{1}{a} \in \left\lbrack \frac{1}{5};\frac{1}{3} \right\rbrack.\]

\[8 \leq b \leq 10\]

\[\frac{1}{b} \in \left\lbrack \frac{1}{10};\frac{1}{8} \right\rbrack.\]

\[24 \leq c \leq 30\]

\[\frac{1}{c} \in \left\lbrack \frac{1}{30};\frac{1}{24} \right\rbrack.\]

\[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} =\]

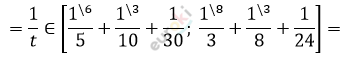
\[= \left\lbrack \frac{10}{30};\frac{12}{24} \right\rbrack = \left\lbrack \frac{1}{3};\frac{1}{2} \right\rbrack.\]

\[То\ есть\ t \in \lbrack 2;3\rbrack.\]

\[Ответ:t \in \lbrack 2;3\rbrack.\]