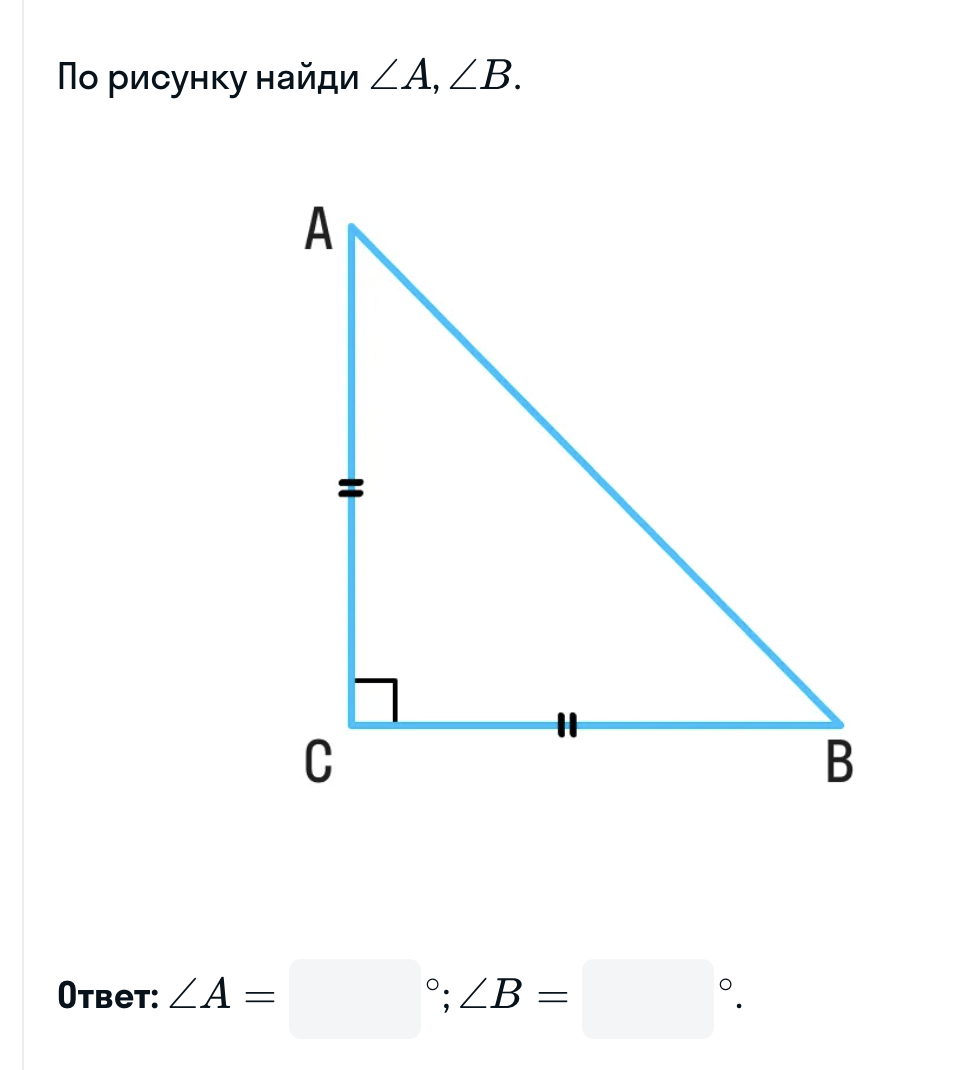
По рисунку найди \(\angle A\), \(\angle B\).

Здравствуйте, ребята! Давайте решим эту задачу вместе. 1. Анализ условия. * Мы видим прямоугольный треугольник \(\triangle ABC\), где \(\angle C = 90^{\circ}\). * Стороны \(AC\) и \(BC\) равны (указано двумя чёрточками), значит, \(\triangle ABC\) является равнобедренным. 2. Основные знания. * Сумма углов треугольника равна \(180^{\circ}\). * В равнобедренном треугольнике углы при основании равны. 3. Решение. * Так как \(\triangle ABC\) прямоугольный, то \(\angle A + \angle B + \angle C = 180^{\circ}\). * \(\angle A + \angle B = 180^{\circ} - \angle C = 180^{\circ} - 90^{\circ} = 90^{\circ}\). * Поскольку \(\triangle ABC\) равнобедренный и \(AC = BC\), то \(\angle A = \angle B\). * Значит, \(\angle A = \angle B = \frac{90^{\circ}}{2} = 45^{\circ}\). 4. Ответ. * \(\angle A = 45^{\circ}\) * \(\angle B = 45^{\circ}\) Итоговый ответ: \(\angle A = 45^{\circ}\); \(\angle B = 45^{\circ}\).