Площадь прямоугольника 360 см^2. Если одну его сторону увеличить на 3 см, а другую уменьшить на 6 см, то получится равновеликий ему прямоугольник. Найдите стороны первого прямоугольника.

\[\left\{ \begin{matrix} xy = 360\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ (x + 3)(y - 6) = 360 \\ \end{matrix} \right.\ \text{\ \ }\]

\[\left\{ \begin{matrix} x = \frac{360}{y}\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \left( \frac{360}{y} + 3 \right)(y - 6) = 360 \\ \end{matrix} \right.\ \]

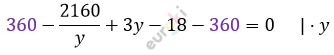
\[- 2160 + 3y^{2} - 18y = 0\ \ \ \ \ |\ :3\]

\[y^{2} - 6y - 720 = 0\]

\[D = ( - 6)^{2} - 4 \cdot 1 \cdot ( - 720) =\]

\[= 36 + 2880 = 2916;\ \ \ \ \]

\[\sqrt{D} = 54.\]

\[y_{1} = \frac{6 + 54}{2} = \frac{60}{2} = 30;\ \]

\[y_{2} = \frac{6 - 54}{2} = \frac{- 48}{2} =\]

\[= - 24\ \ (не\ подходит).\]

\[x_{1} = \frac{360}{30} = 12.\]

\[Ответ:12\ см\ и\ 30\ см.\]