Первая бригада работала на ремонте дороги 9 ч, после чего к ней присоединилась вторая бригада. Через 6 ч совместной работы была отремонтирована 1/2 дороги. За сколько часов может отремонтировать дорогу каждая бригада самостоятельно, если второй бригаде для этого требуется на 9 ч меньше, чем первой?

Ответ:

\[Пусть\ x\ часов - надо\ первой\ \]

\[бригаде,\ \]

\[(x - 9)\ часов - надо\ второй\ \]

\[бригаде.\]

\[1 - вся\ дорога.\]

\[Вместе\ бригады\ \]

\[отремонтировали\ \frac{1}{2}\ часть\ \]

\[дороги.\]

\[Составим\ уравнение:\ \]

\[\frac{9}{x} + 6 \cdot \left( \frac{1}{x} + \frac{1}{x - 9} \right) = \frac{1}{2}\]

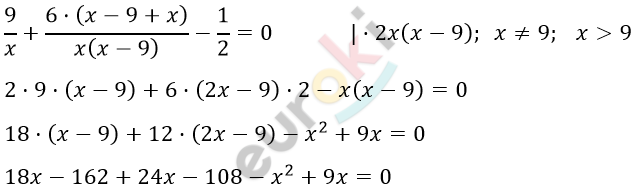
\[- x^{2} + 51x - 270 = 0\ \ | \cdot ( - 1)\]

\[x^{2} - 51x + 270 = 0\]

\[x_{1} + x_{2} = 51;\ \ \ x_{1} \cdot x_{2} = 270.\]

\[x_{1} = 45\ (ч) - может\ \]

\[отремонтировать\ дорогу\ \]

\[первая\ бригада.\ \ \]

\[x_{2} = 6\ (не\ подходит).\]

\[x - 9 = 45 - 9 = 36\ (ч) -\]

\[может\ отремонтировать\ \]

\[дорогу\ вторая\ бригада.\]

\[Ответ:45\ часов\ и\ 36\ часов.\]