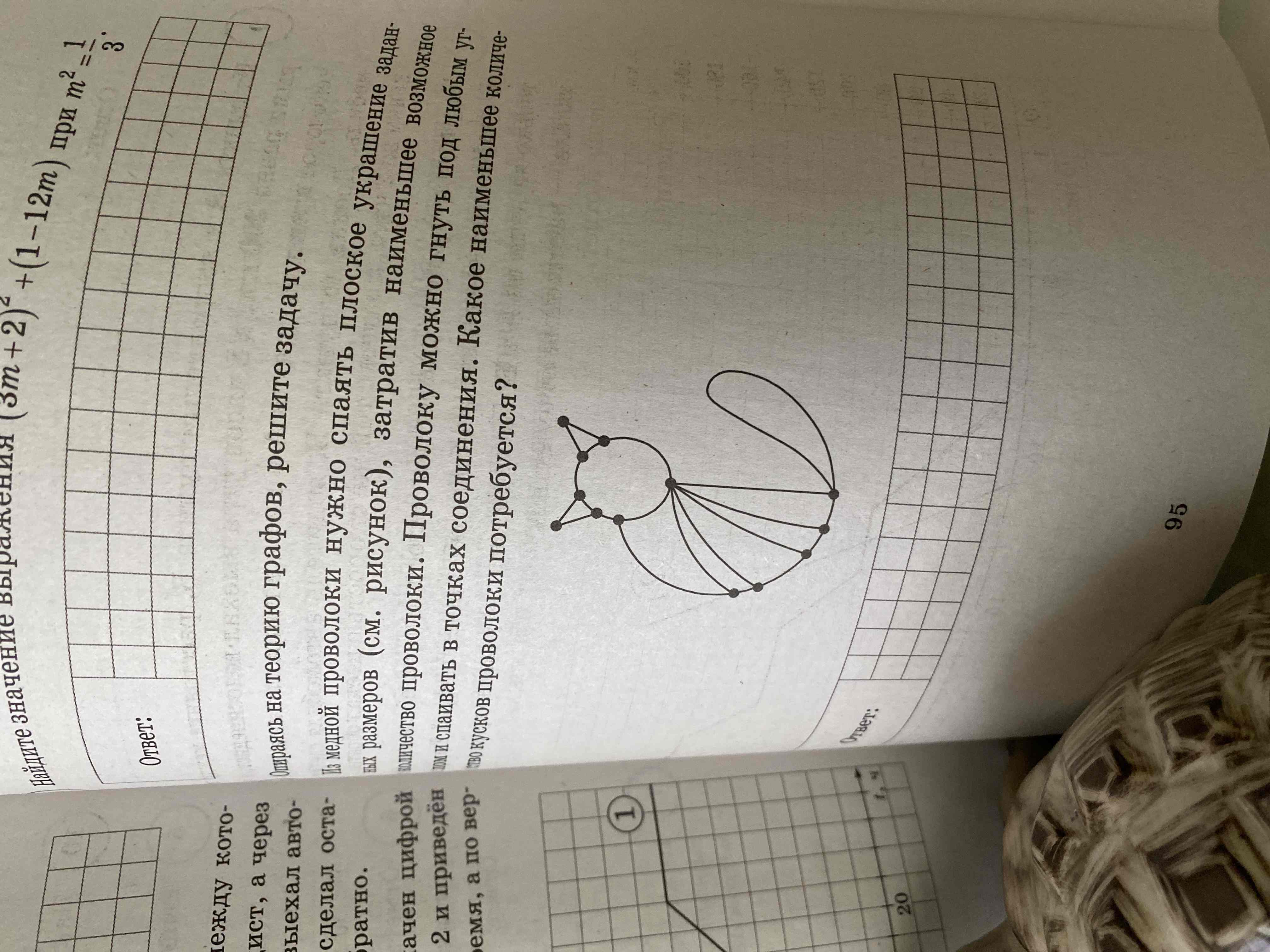
Вопрос:
Опираясь на теорию графов, решите задачу. Из медной проволоки нужно спаять плоское украшение заданных размеров (см. рисунок), затратив наименьшее возможное количество проволоки. Проволоку можно гнуть под любым углом и спаивать в точках соединения. Какое наименьшее количество кусков проволоки потребуется?
Ответ:
Задача сводится к определению минимального количества кусков проволоки, необходимого для создания графа, изображенного на рисунке, при условии, что проволоку можно спаивать в точках соединения.
В теории графов, задача нахождения минимального количества кусков проволоки, необходимого для обхода графа, связана с понятием эйлерова пути. Эйлеров путь существует, если в графе не более двух вершин с нечётной степенью. Если таких вершин нет, то существует эйлеров цикл, и можно обойти граф одним куском проволоки. Если есть две вершины с нечётной степенью, то эйлеров путь начинается в одной из этих вершин и заканчивается в другой.
Если же в графе больше двух вершин с нечётной степенью, то для каждой пары таких вершин потребуется дополнительный кусок проволоки, чтобы обойти граф.
Посчитаем степени вершин в данном графе:
1. Верхняя левая вершина: степень 1 (нечётная)
2. Верхняя правая вершина: степень 1 (нечётная)
3. Нижняя левая вершина: степень 1 (нечётная)
4. Нижняя правая вершина: степень 1 (нечётная)
5. Левая вершина посередине: степень 3 (нечётная)
6. Правая вершина посередине: степень 3 (нечётная)
7. Центральная вершина: степень 6 (чётная)
Мы видим, что в графе 6 вершин с нечётной степенью. Чтобы обойти граф, нужно разбить эти вершины на пары. Каждая пара требует одного дополнительного куска проволоки.
Количество пар: 6 / 2 = 3
Значит, нам потребуется 3 куска проволоки.
Ответ: 3