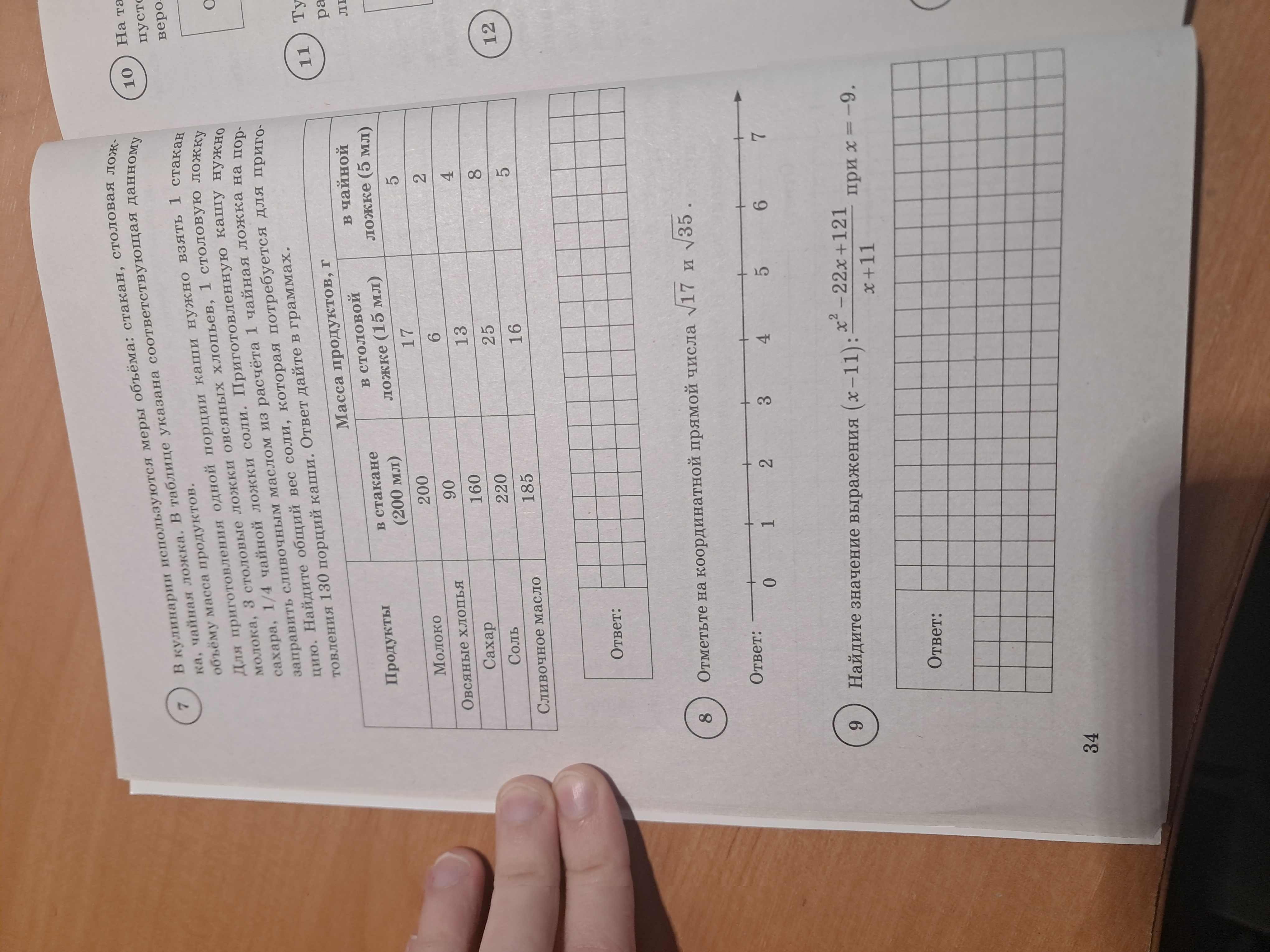
Вопрос:
Найдите значение выражения $(x-11): \frac{x^2 - 22x + 121}{x+11}$ при $x = -9$.
Ответ:
1. **Преобразуем выражение:**
Выражение можно переписать как: $(x-11) : \frac{(x-11)^2}{x+11}$.
Это эквивалентно: $(x-11) * \frac{x+11}{(x-11)^2}$.
2. **Сократим выражение:**
Сокращаем $(x-11)$ в числителе и знаменателе: $\frac{x+11}{x-11}$.
3. **Подставим значение x = -9:**
$\frac{-9+11}{-9-11} = \frac{2}{-20} = -\frac{1}{10} = -0.1$.
**Ответ: -0.1**
Похожие
- Заполните таблицу. В кулинарии используются меры объёма: стакан, столовая ложка, чайная ложка. В таблице указана соответствующая данному объёму масса продуктов.
- Найдите общий вес соли, которая потребуется для приготовления 130 порций каши.
- Отметьте на координатной прямой числа $\sqrt{17}$ и $\sqrt{35}$.
- Найдите значение выражения $(x-11): \frac{x^2 - 22x + 121}{x+11}$ при $x = -9$.