Найдите значение выражения: (1/x+1/y)*(x-y)/корень из 2 при x= корень 4 степени из (5+2 корень из 6), y= корень 4 степени из (5-2корень из 6).

\[\left( \frac{1}{x} + \frac{1}{y} \right) \cdot \frac{x - y}{\sqrt{2}} =\]

\[= \frac{(x + y)(x - y)}{\text{xy}\sqrt{2}} = \frac{x^{2} - y^{2}}{\sqrt{2}\text{xy}}\ \]

\[x = \sqrt[4]{5 + 2\sqrt{6}};\ \ \ y = \sqrt[4]{5 - 2\sqrt{6}}:\]

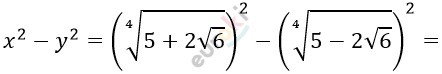
\[= \sqrt{5 + 2\sqrt{6}} - \sqrt{5 - 2\sqrt{6}} =\]

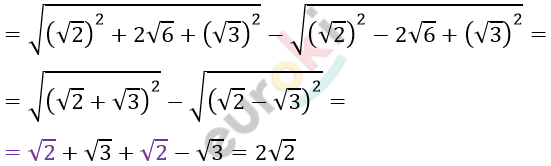
\[xy = \sqrt[4]{5 + 2\sqrt{6}} \cdot \sqrt[4]{5 - 2\sqrt{6}} =\]

\[= \sqrt[4]{\left( 5 + 2\sqrt{6} \right)\left( 5 - 2\sqrt{6} \right)} =\]

\[= \sqrt[4]{\left( \sqrt{2} + \sqrt{3} \right)^{2} \cdot \left( \sqrt{2} - \sqrt{3} \right)^{2}} =\]

\[= \sqrt[4]{\left( \left( \sqrt{2} + \sqrt{3} \right)\left( \sqrt{2} - \sqrt{3} \right) \right)} =\]

\[= \sqrt[4]{\left( \left( \sqrt{2} \right)^{2} - \left( \sqrt{3} \right)^{2} \right)} =\]

\[= \sqrt[4]{(2 - 3)^{2}} = \sqrt[4]{( - 1)^{2}} = 1\]

\[\frac{x^{2} - y^{2}}{\sqrt{2}\text{xy}} = \frac{2\sqrt{2}}{\sqrt{2} \cdot 1} = 2.\]