Найдите стороны прямоугольника, если их разность равна 21 см, а диагональ прямоугольника — 39 см.

Ответ:

\[Пусть\ x\ см - одна\ сторона\ \]

\[прямоугольника;\ \]

\[(x + 21)\ см - другая\ сторона.\]

\[Диагональ\ равна\ 39\ см.\]

\[Составим\ уравнение,\ \]

\[используя\ теорему\ Пифагора:\ \]

\[x^{2} + (x + 21)^{2} = 39^{2}\]

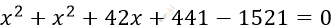
\[2x² + 42x - 1080 = 0\ \ |\ :2\]

\[x^{2} + 21x - 540 = 0\]

\[D = 21^{2} - 4 \cdot 1 \cdot ( - 540) =\]

\[= 441 + 2160 = 2601\]

\[x_{1} = \frac{- 21 + 51}{2} = \frac{30}{2} =\]

\[= 15\ (см) - одна\ сторона\ \]

\[прямоугольника.\ \]

\[x_{2} = \frac{- 21 - 51}{2} = - \frac{72}{2} =\]

\[= - 36\ (не\ подходит)\]

\[x + 21 = 15 + 21 = 36\ (см) -\]

\[вторая\ сторона\ \]

\[прямоугольника.\]

\[Ответ:15\ см\ и\ 36\ см.\]