Найдите наименьшее целое решение неравенства 2/7x-1>x-2/7, удовлетворяющее неравенству x^2<17.

\[\left\{ \begin{matrix} \frac{2}{7}x - 1 > x - \frac{2}{7}\ \ | \cdot 7 \\ x^{2} < 17\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 2x - 7 > 7x - 2\ \\ - \sqrt{17} < x < \sqrt{17} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} 7x - 2x < - 7 + 2 \\ - \sqrt{17} < x < \sqrt{17}\ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} 5x < - 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ - \sqrt{17} < x < \sqrt{17} \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ }\]

\[\left\{ \begin{matrix} x < - 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ - \sqrt{17} < x < \sqrt{17} \\ \end{matrix} \right.\ \]

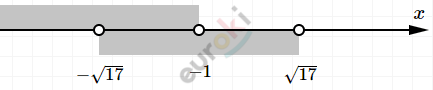
\[Ответ:\ - 4.\]