Решите неравенство: (13-2корень из 22)x>корень из 11-корень из 2.

\[\left( 13 - 2\sqrt{22} \right)x > \sqrt{11} - \sqrt{2}\]

\[\left( \sqrt{11} - \sqrt{2} \right)^{2}x > \sqrt{11} - \sqrt{2}\]

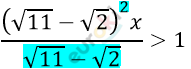
\[\left( \sqrt{11} - \sqrt{2} \right)x > 1\]

\[x > \frac{1}{\sqrt{11} - \sqrt{2}}\]

\[\frac{1}{\sqrt{11} - \sqrt{2}} =\]

\[= \frac{\sqrt{11} + \sqrt{2}}{\left( \sqrt{11} - \sqrt{2} \right)\left( \sqrt{11} + \sqrt{2} \right)} =\]

\[= \frac{\sqrt{11} + \sqrt{2}}{11 - 2} = \frac{\sqrt{11} + \sqrt{2}}{9}\]

\[x > \frac{\sqrt{11} + \sqrt{2}}{9}\]

\[Ответ:\ \ \left( \frac{\sqrt{11} + \sqrt{2}}{9}; + \infty \right).\]