Найдите четыре последовательных натуральных числа таких, что произведение второго и четвёртого из этих чисел на 45 больше произведения первого и третьего.

\[Пусть\ x,\ x + 1,\ x + 2,\ \]

\[x + 3 - четыре\ \]

\[последовательных\ \]

\[натуральных\ числа.\ \]

\[Тогда:\ \]

\[(x + 1)(x + 3) - x(x + 2) = 45\]

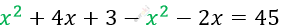
\[2x = 42\]

\[x = 21 - первое\ число.\]

\[x + 1 = 21 + 1 = 22 - второе\ \]

\[число.\]

\[x + 2 = 21 + 2 = 23 - третье\ \]

\[число.\]

\[x + 3 = 21 + 3 =\]

\[= 24 - четвертое\ число.\]

\[Ответ:числа\ 21,\ 22,\ 23,\ 24.\]