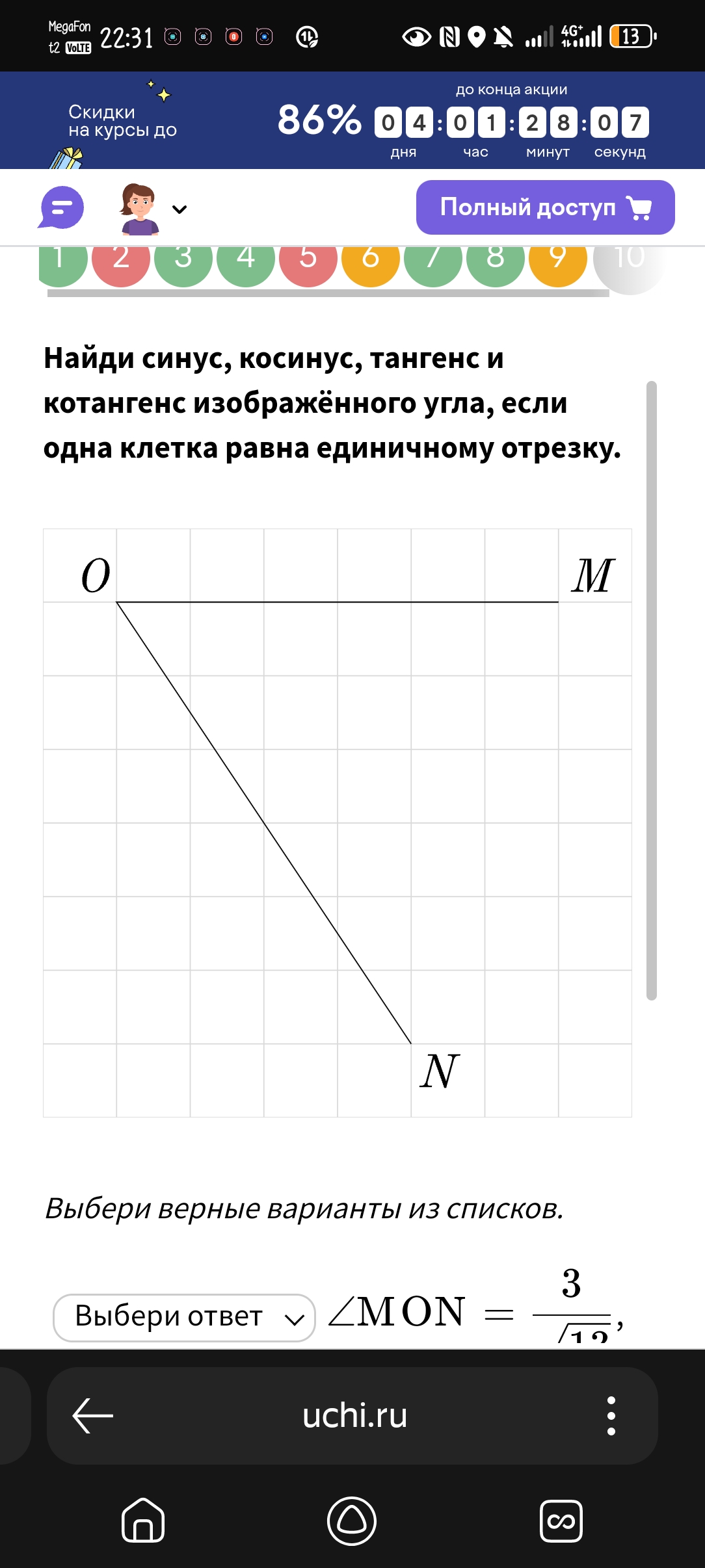
Найди синус, косинус, тангенс и котангенс изображённого угла, если одна клетка равна единичному отрезку. Выбери верные варианты из списков. ∠MON = 3/√10

Для начала, определим длины сторон прямоугольного треугольника $\triangle MON$. По условию, каждая клетка равна единичному отрезку. * $OM = 3$ * $MN = 1$ Теперь найдем гипотенузу $ON$ с помощью теоремы Пифагора: $ON = \sqrt{OM^2 + MN^2} = \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10}$ Теперь мы можем найти синус, косинус, тангенс и котангенс угла $MON$. * Синус угла $MON$ ($\sin(\angle MON)$) – это отношение противолежащего катета к гипотенузе: $\sin(\angle MON) = \frac{MN}{ON} = \frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10}$ * Косинус угла $MON$ ($\cos(\angle MON)$) – это отношение прилежащего катета к гипотенузе: $\cos(\angle MON) = \frac{OM}{ON} = \frac{3}{\sqrt{10}} = \frac{3\sqrt{10}}{10}$ * Тангенс угла $MON$ ($\tan(\angle MON)$) – это отношение противолежащего катета к прилежащему катету: $\tan(\angle MON) = \frac{MN}{OM} = \frac{1}{3}$ * Котангенс угла $MON$ ($\cot(\angle MON)$) – это отношение прилежащего катета к противолежащему катету: $\cot(\angle MON) = \frac{OM}{MN} = \frac{3}{1} = 3$ **Ответ:** $\sin(\angle MON) = \frac{\sqrt{10}}{10}$ $\cos(\angle MON) = \frac{3\sqrt{10}}{10}$ $\tan(\angle MON) = \frac{1}{3}$ $\cot(\angle MON) = 3$