Решите уравнение x^3+x^2+bx-24=0, если известно, что один из его корней равен -2.

\[x^{3} + x^{2} + bx - 24 = 0\]

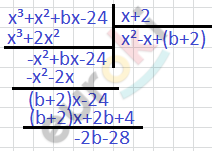
\[Так\ как\ ( - 2) - корень\ \Longrightarrow\]

\[\Longrightarrow - 2b - 28 = 0\]

\[- 2b - 28 = 0\]

\[- 2b = 28\]

\[b = - 14.\]

\[x^{3} + x^{2} - 14x - 24 = 0\]

\[x^{2} - x + (b + 2) = x^{2} - x - 12\]

\[(x + 2)\left( x^{2} - x - 12 \right) = 0\]

\[x + 2 = 0\]

\[x = - 2.\]

\[x^{2} - x - 12 = 0\]

\[D = ( - 1)^{2} - 4 \cdot 1 \cdot ( - 12) =\]

\[= 1 + 48 = 49;\ \ \ \sqrt{D} = 7.\]

\[x_{1} = \frac{1 + 7}{2} = \frac{8}{2} = 4;\ \ \ \ \ \]

\[\ x_{2} = \frac{1 - 7}{2} = \frac{- 6}{2} = - 3\]

\[Ответ:\ - 2;4;\ - 3.\]