Квадрат разности цифр данного числа равен 9. Разность квадратов данного числа и числа, записанного теми же цифрами, но в обратном порядке, равна 1485. Найдите данное число.

\[Пусть\ x - цифра\ единиц\ \]

\[двузначного\ числа,\ тогда\ y -\]

\[цифра\ десятков\ этого\ же\ \]

\[числа.\ \]

\[Составим\ и\ решим\ систему\ \]

\[уравнений:\]

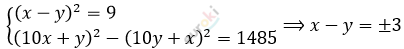
\[9 \cdot 11 \cdot (x + y)(x - y) =\]

\[= 9 \cdot 11 \cdot 15\]

\[\pm 3 \cdot (x + y) = 15\ \ \ \ \ \ |\ :( \pm 3)\]

\[x + y = \pm 5\]

\[\left\{ \begin{matrix} x - y = \pm 3 \\ x + y = \pm 5 \\ \end{matrix} \right.\ \]

\[x_{1} = 4 \Longrightarrow y_{1} = 1\]

\[x_{2} = - 4 \Longrightarrow y_{2} = - 2\]

\[Отрицательные\ числа\ \]

\[не\ подходят,\ искомое\ число\ \]

\[равно\ 41.\]

\[Ответ:\ \ 41.\]