Изобразите на координатной плоскости множество решений системы неравенств x^2+y^2<=16; y>=x. Найдите площадь полученной фигуры.

Ответ:

\[\left\{ \begin{matrix} x^{2} + y^{2} \leq 16\ \\ y \geq x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]

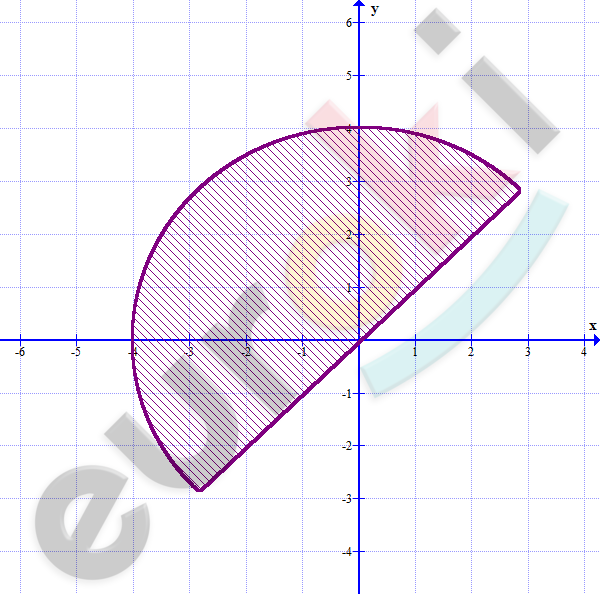
\[Получили\ полукруг,\ с\ радиусом = 4.\]

\[S = \frac{\pi \cdot 4^{2}}{2} = \frac{16\pi}{2} = 8\pi.\]

\[Ответ:полукруг;8\pi.\]