Из двух пунктов, расстояние между которыми равно 18 км, вышли одновременно на встречу друг другу две группы туристов и встретились через 2 ч. Определите, с какой скоростью шла каждая группа, если известно, что на прохождение всего пути одной из них потребовалось на 54 мин больше, чем другой.

\[Пусть\ x\ \frac{км}{ч} - скорость\ \]

\[одной\ группы,\ тогда\ y\ \frac{км}{ч} -\]

\[скорость\ второй\ группы.\]

\[(x + y) = 18\ :2 = 9\ \frac{км}{ч} -\]

\[скорость\ сближения.\]

\[По\ условию\ известно:\]

\[\frac{18}{x} = \frac{18}{y} + \frac{9}{10}\]

\[Составим\ систему\ уравнений:\]

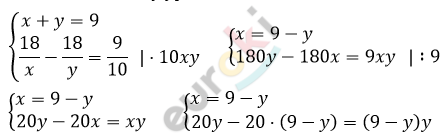
\[20y - 180 + 20y = 9y - y^{2}\]

\[y^{2} + 40y - 9y - 180 = 0\]

\[y^{2} + 31y - 180 = 0\]

\[D = 961 + 720 = 1681 = 41^{2}\]

\[y_{1} = \frac{- 31 - 41}{2} = - \frac{72}{2} =\]

\[= - 36 < 0\ (не\ подходит).\]

\[y_{2} = \frac{- 31 + 41}{2} = \frac{10}{2} =\]

\[= 5\ \left( \frac{км}{ч} \right) - скорость\ второй\ \]

\[группы.\]

\[x = 9 - y = 9 - 5 = 4\ \left( \frac{км}{ч} \right) -\]

\[скорость\ первой\ группы.\]

\[Ответ:\ \ 4\ \frac{км}{ч}\ и\ 5\ \frac{км}{ч}.\]