Две трубы, действуя одновременно, заливают цистерну нефтью за 2 ч. За сколько часов заполняет цистерну первая труба, действуя отдельно, если ей для залива цистерны требуется на 3 ч меньше, чем другой?

\[Пусть\ x\ часов\ заполняет\ \]

\[первая\ труба;\ \ тогда\ \text{y\ }часов -\]

\[вторая\ труба.\]

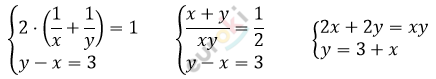
\[2x + 2 \cdot (3 + x) = x(3 + x)\]

\[2x + 6 + 2x = 3x + x^{2}\]

\[x^{2} - x - 6 = 0\]

\[D = 1 + 24 = 25\]

\[x_{1} = \frac{1 + 5}{2} = 3;\ \ \ \ \ \ \]

\[x_{2} = \frac{1 - 5}{2} = - 2\ (не\ подходит)\]

\[y_{1} = 3 + 3 = 6;\ \ \ \ \ \ \]

\[y_{2} = 3 + ( - 2) =\]

\[= 1\ (не\ подходит).\]

\[Ответ:3\ часа\ нужно\ первой\ \]

\[трубе;6\ часов\ нужно\ второй\ \]

\[трубе.\]