Вопрос:
Докажите неравенство: x^2-4xy+5y^2+2y+2>0.
Ответ:
\[x² - 4xy + 5y^{2} + 2y + 2 > 0\]
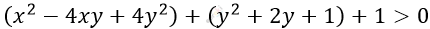
\[(x - 2y)^{2} + (y + 1)^{2} + 1 > 0\]
\[(x - 2y)^{2} \geq 0;\ \ (y + 1)^{2} \geq 0;\ \ \]
\[1 > 0 \Longrightarrow верно.\]
\[x² - 4xy + 5y^{2} + 2y + 2 > 0\]
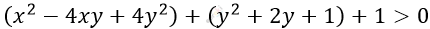
\[(x - 2y)^{2} + (y + 1)^{2} + 1 > 0\]
\[(x - 2y)^{2} \geq 0;\ \ (y + 1)^{2} \geq 0;\ \ \]
\[1 > 0 \Longrightarrow верно.\]