Вопрос:
Докажите неравенство: x^2-4x+y^2+2y+5>=0.
Ответ:
\[x² - 4x + y^{2} + 2y + 5 \geq 0\]
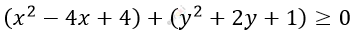
\[(x - 2)^{2} + (y + 1)^{2} \geq 0\]
\[(x - 2)^{2} \geq 0;\ \ \]
\[(y + 1)^{2} \geq 0 \Longrightarrow верно.\]
Похожие
- 1. Ты услышишь сообщение. Для каждого предложения А-Е выбери один правильный вариант ответа на трех предложенных (1, 2 или 3). Ты услышишь текст дважды. A. Andy is 1) a new teacher. 2) a pupil. 3) a boy's father. B. Andy likes to 1) read books. 2) learn new words. 3) watch films. C. What subject does Andy like? 1) German 2) Literature 3) Maths D. At the German lesson Andy hopes to 1) learn new words. 2) read about English schools. 3) watch a film. E. After the lessons and before lunch Andy wants to 1) go to his friend. 2) watch a film about animals. 3) do his homework. Запиши в таблицу выбранные цифры под соответствующими буквами.
- Задача:
- Решение: