Докажите неравенство: a^2+8a+17>0.

Ответ:

\[a² + 8a + 17 > 0\]

\[a^{2} + 8a + 17 = 0\]

\[1)\ D = b² - 4ac =\]

\[= 64 - 4 \cdot 1 \cdot 17 =\]

\[= 64 - 68 < 0 \Longrightarrow нет\ корней.\]

\[2)\ x_{0} = \frac{- b}{2a} = - \frac{8}{2} = - 4\]

\[y_{0}( - 4) = 16 - 32 + 17 =\]

\[= 33 - 32 = 1 \Longrightarrow ( - 4;1).\]

\[3)\ a = 1 > 0 \Longrightarrow ветви\ вверх.\]

\[4)\ эскиз\ графика:\ \]

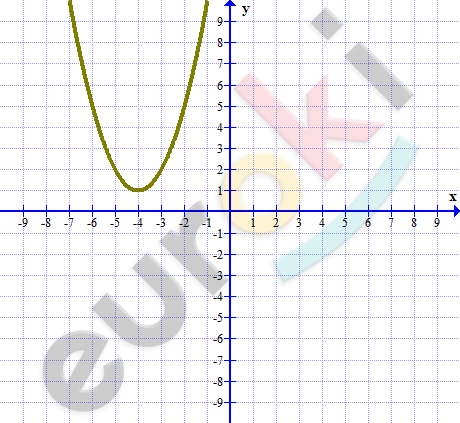
\[При\ любом\ значении\ a \Longrightarrow\]

\[\Longrightarrow a^{2} + 8a + 17 > 0.\]