Докажите, что выражение (а-b)(a-b+4)+4принимает неотрицательные значения при любых значениях переменных.

\[(a - b)(a - b + 4) + 4 =\]

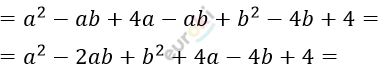
\[= (a - b)^{2} + 4 \cdot (a - b) + 4 =\]

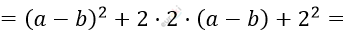
\[= \left( (a - b) + 2 \right)^{2} =\]

\[= (a - b + 2)^{2} \geq 0\ при\ любых\ \]

\[a\ и\ b.\ \]

\[Что\ и\ требовалось\ доказать.\]