Для каждого значения параметра a решите неравенство x^2-(3a-2)x+2a^2-a-3>0.

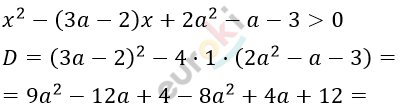
\[= a^{2} - 8a + 16 = (a - 4)^{2};\ \ \ \ \ \ \ \ \]

\[x_{1} = 2a - 3;\ \ \ \ x_{2} = a + 1.\]

\[1)\ Если\ 2a - 3 = a + 1,\ \]

\[то\ есть\ a = 4;\ \ \]

\[то\ неравенство\ можно\ \]

\[переписать\ в\ виде:\]

\[(x - 5)^{2} > 0 \Longrightarrow решения:\]

\[x \in ( - \infty;5) \cup (5; + \infty).\]

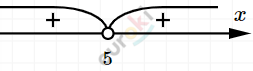
\[2)\ 2a - 3 < a + 1\ \ \]

\[то\ есть\ a < 4;\ \ \Longrightarrow решения:\ \]

\[\ x \in ( - \infty;2a - 3) \cup (a + 1; + \infty).\]

\[3)\ 2a - 3 < a + 1\ \ \]

\[то\ есть\ a < 4;\ \ \Longrightarrow решения:\ \ \]

\[x \in ( - \infty;a + 1) \cup (2a - 3; + \infty).\]

\[Ответ:( - \infty;5) \cup (5; + \infty)\ \]

\[при\ a = 4;\ \]

\[( - \infty;2a - 3) \cup (a + 1; + \infty)\ \]

\[при\ a < 4;\ \ \]

\[( - \infty;a + 1) \cup (2a - 3; + \infty)\ \]

\[при\ \ a > 4.\]