Для каждого значения a решите систему неравенств: x^2-8x-9<=0; x>a.

\[\left\{ \begin{matrix} x^{2} - 8x - 9 \leq 0 \\ x > a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[x^{2} - 8x - 9 = 0\]

\[x_{1} + x_{2} = 8,\ \ x_{1} \cdot x_{2} = - 9,\ \ \]

\[x_{1} = 9,\ \ x_{2} = - 1\]

\[(x + 1)(x - 9) \leq 0\]

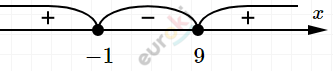
\[- 1 \leq x \leq 9.\]

\[Если\ a < - 1:\ \]

\[- 1 \leq x \leq 9.\]

\[Если\ a \geq 9:\]

\[x \in \varnothing.\]

\[Если\ \ - 1 \leq a < 9:\]

\[a < x \leq 9.\]